Question

5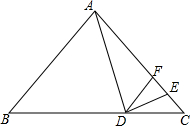．如图，在等腰△ABC中，AB=AC，D是BC边上的一点，且∠ADE=∠AED，DE平分∠CDF，下列结论：①若∠EDC=20°，则∠BAD=40°；②∠DFC=∠ADB；③DF∥AB；④过D分别作△ABD、△ACD的高，长度分别为h₁、h₂，△ABC一腰上的高的长为h，则h₁+h₂=h，其中正确的个数是（　　）

• A． 1
• B． 2
• C． 3
• D． 4

Answer 1

分析 根据三角形的内角和得到∠BAD=∠ADC-∠B，根据等腰三角形的性质得到∠B=∠C，∠CDE=20°，于是得到∠BAD=∠ADE+20°-∠B=∠B+20°+20°-∠B=40°；故①正确；根据角平分线的定义得到∠FDC=2∠CDE=40°=∠ADB，根据三角形的内角和得到∠DFC=∠ADB；故②正确；由于∠B≠∠FDC，于是得到DF不一定与AB平行；故③错误；过B作BH⊥AC于H，DM⊥AB于N，DN⊥AC于N，根据三角形的面积即可得到h₁+h₂=h，故④正确．

解答 解：∵在△ABD中，∠BAD=180°-∠B-∠ADB，
∠ADB=180°-∠ADC，
∴∠BAD=∠ADC-∠B，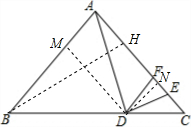
∵AB=AC，
∴∠B=∠C，∠CDE=20°，且∠AED=∠ADE，
∴∠BAD=∠ADE+20°-∠B=∠B+20°+20°-∠B=40°；故①正确；
∵DE平分∠CDF，
∴∠FDC=2∠CDE=40°=∠ADB，
∵AB=AC，
∴∠C=∠B，
∴∠ADB=180°-∠B-∠BAD，∠DFC=180°-∠FDC-∠C，
∴∠DFC=∠ADB；故②正确；
∵∠DFC=∠ADB，
∵∠B≠∠BAD，
∴∠B≠∠FDC，
∴DF不一定与AB平行；故③错误；
过B作BH⊥AC于H，DM⊥AB于N，DN⊥AC于N，
∴BH=h，DM=h₁，DN=h₂，
∴S_△ABC=S_△ABD+S_△ACD，
即$\frac{1}{2}$AC•h=$\frac{1}{2}$AB•h₁+$\frac{1}{2}$AC•h₂，
∵AB=AC，
∴h₁+h₂=h，
故④正确；
故选C．

点评 此题主要考查等腰三角形的性质和三角形内角和定理的理解和掌握，难易程度适中，适合学生的训练，是一道典型的题目．