题目内容
1.解下列方程:(1)3x(x-2)=2(x-2)
(2)3x2-1=6x (用配方法)
分析 (1)移项后分解因式,即可得出两个一元一次方程,求出方程的解即可;
(2)移项,配方,开方,即可得出两个一元一次方程,求出方程的解即可.
解答 解:(1)移项,得3x(x-2)-2(x-2)=0,
分解因式,得(x-2)(3x-2)=0,
解得x1=2,x2=$\frac{2}{3}$;
(2)3x2-1=6x,
移项,得3x2-6x=1,
两边除以3,得x2-2x=$\frac{1}{2}$,
x2-2x+1=$\frac{3}{2}$,
(x-1)2=$\frac{3}{2}$,
解得x1=1+$\frac{\sqrt{6}}{2}$,x2=1-$\frac{\sqrt{6}}{2}$.
点评 本题考查了因式分解法解一元二次方程,因式分解法就是先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了.也考查了配方法解方程.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
12.甲乙平均数均是7,甲的方差是1.2,乙的方差是5.8,下列说法中不正确的是( )
| A. | 甲、乙射中的总环数相同 | B. | 甲的成绩稳定 | ||
| C. | 乙的成绩波动较大 | D. | 甲、乙的众数相同 |
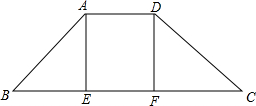 梯形ABCD中,AD∥BC,AE⊥BC于点E,DF⊥BC于点F,∠B=∠C=45°,AD=AE=2,CD=2$\sqrt{2}$,动点P从点C出发以每秒1个单位长度的速度沿这线段CD-DA-AB运动,当点P到达点B时停止运动,运动过程中,点P作BC的垂线与BC交于点Q,设直线PQ扫过梯形ABCD的面积为S,点P运动的时间为t.
梯形ABCD中,AD∥BC,AE⊥BC于点E,DF⊥BC于点F,∠B=∠C=45°,AD=AE=2,CD=2$\sqrt{2}$,动点P从点C出发以每秒1个单位长度的速度沿这线段CD-DA-AB运动,当点P到达点B时停止运动,运动过程中,点P作BC的垂线与BC交于点Q,设直线PQ扫过梯形ABCD的面积为S,点P运动的时间为t. 如图,∠AOB=30°,P是∠AOB内一点,PO=5,Q、R分别是OA、OB上的动点,求△PQR周长的最小值5.
如图,∠AOB=30°,P是∠AOB内一点,PO=5,Q、R分别是OA、OB上的动点,求△PQR周长的最小值5.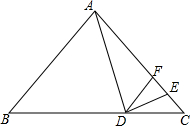 如图,在等腰△ABC中,AB=AC,D是BC边上的一点,且∠ADE=∠AED,DE平分∠CDF,下列结论:①若∠EDC=20°,则∠BAD=40°;②∠DFC=∠ADB;③DF∥AB;④过D分别作△ABD、△ACD的高,长度分别为h1、h2,△ABC一腰上的高的长为h,则h1+h2=h,其中正确的个数是( )
如图,在等腰△ABC中,AB=AC,D是BC边上的一点,且∠ADE=∠AED,DE平分∠CDF,下列结论:①若∠EDC=20°,则∠BAD=40°;②∠DFC=∠ADB;③DF∥AB;④过D分别作△ABD、△ACD的高,长度分别为h1、h2,△ABC一腰上的高的长为h,则h1+h2=h,其中正确的个数是( )