题目内容
某校为美化校园,准备在长32m,宽20m的长方形场地上修建宽度相等的一条东西方向、两条南北方向的长方形花廊,余下部分作为活动场所,要求余下的活动场所总面积为442m2,甲、乙两种设计方案如图所示.
(1)分别求出这两种方案中花圃的宽度.
(2)比较你所列的两个方程,方案甲可以转化为方案乙求解吗?为什么?

(1)分别求出这两种方案中花圃的宽度.
(2)比较你所列的两个方程,方案甲可以转化为方案乙求解吗?为什么?

考点:一元二次方程的应用
专题:几何图形问题
分析:(1)设设计方案中花圃的宽为xm,然后表示出花圃的宽度和长度,再根据余下的活动场所总面积为442m2,列出方程.
(2)根据(1)中的所列方程可得利用平移把小路平移到长方形场地的两个边上,再列出方程即可.
(2)根据(1)中的所列方程可得利用平移把小路平移到长方形场地的两个边上,再列出方程即可.
解答:解:(1)设甲设计方案中花圃的宽为xm,由题意得:
(32-2x)(20-x)=442,
解得:x1=3,x2=33(不合题意舍去),
20-3=17(米),
答:甲设计方案中花圃的宽为17m;
设乙设计方案中花圃的宽为ym,由题意得:
(32-2y)(20-y)=442,
解得:y1=3,y2=33(不合题意舍去),
20-3=17(米),
答:甲设计方案中花圃的宽为17m;
(2)方案甲可以转化为方案乙求解,利用平移方法可以把小路平移到长方形场地的两个边上,然后表示花圃的宽和长,根据面积是442m2可得方程.
(32-2x)(20-x)=442,
解得:x1=3,x2=33(不合题意舍去),
20-3=17(米),
答:甲设计方案中花圃的宽为17m;
设乙设计方案中花圃的宽为ym,由题意得:
(32-2y)(20-y)=442,
解得:y1=3,y2=33(不合题意舍去),
20-3=17(米),
答:甲设计方案中花圃的宽为17m;
(2)方案甲可以转化为方案乙求解,利用平移方法可以把小路平移到长方形场地的两个边上,然后表示花圃的宽和长,根据面积是442m2可得方程.
点评:此题主要考查了二元一次方程的应用,关键是正确理解题意,找出题目中的等量关系,列出方程.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列语句是真命题的是( )
| A、大于锐角的角是钝角 |
| B、如果一个实数有算术平方根,那么它的算术平方根是整数 |
| C、如果AC=BC,那么点C是线段AB的中点 |
| D、在同一平面,内错角相等,两直线平行 |
下列等式一定成立的是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、(
|
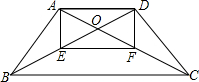 如图,在梯形ABCD中,AD∥BC,AB=CD,对角线AC与BD交于点O,E、F分别为OB、OC的中点.
如图,在梯形ABCD中,AD∥BC,AB=CD,对角线AC与BD交于点O,E、F分别为OB、OC的中点.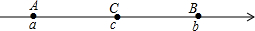 如图,已知数轴上点A、B、C所表示的数分别为a、b、c,点C是线段AB的中点,且AB=2,如果原点O的位置在线段AC上,那么|a+b-2c|等于( )
如图,已知数轴上点A、B、C所表示的数分别为a、b、c,点C是线段AB的中点,且AB=2,如果原点O的位置在线段AC上,那么|a+b-2c|等于( )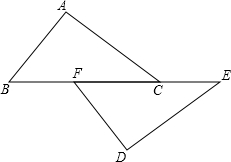 已知:如图,点B、F、C、E在一条直线上,BF=CE,AB∥DE,∠ACB=∠DFE.求证:AC=DF.
已知:如图,点B、F、C、E在一条直线上,BF=CE,AB∥DE,∠ACB=∠DFE.求证:AC=DF.