题目内容
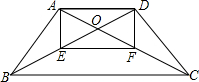 如图,在梯形ABCD中,AD∥BC,AB=CD,对角线AC与BD交于点O,E、F分别为OB、OC的中点.
如图,在梯形ABCD中,AD∥BC,AB=CD,对角线AC与BD交于点O,E、F分别为OB、OC的中点.(1)求证:∠ACB=∠DBC;
(2)若2AD=BC.求证:四边形AEFD为矩形.
考点:三角形中位线定理,矩形的判定,梯形
专题:
分析:(1)要证:∠ACB=∠DBC由等腰梯形的判定定理知,由题意知AB=CD,所以∠ABC=∠DCB,又OB=OC,所以∠OBC=∠OCB即可得证.
(2)要证四边形AEFD为矩形,只需证其对角线相等且相互平分,然后利用平行线分线段成比例定理进行证明.
(2)要证四边形AEFD为矩形,只需证其对角线相等且相互平分,然后利用平行线分线段成比例定理进行证明.
解答:证明:(1)∵在梯形ABCD中,AD∥BC,AB=CD,
∴∠ABC=∠DCB,
又∵OB=OC,
∴∠OBC=∠OCB,
∴∠ACB=∠DBC;
(2)∵E、F分别为OB、OC的中点,
∴EF∥BC,EF=
BC,
∵AD=
BC,AD∥BC,
∴EF∥AD,EF=AD,
∴四边形AEFD是平行四边形,
∴OF=OA,EO=DO,
又OA=OD,
∴OF=OA=EO=DO,
∴四边形AEFD为矩形.
∴∠ABC=∠DCB,
又∵OB=OC,
∴∠OBC=∠OCB,
∴∠ACB=∠DBC;

(2)∵E、F分别为OB、OC的中点,
∴EF∥BC,EF=
| 1 |
| 2 |
∵AD=
| 1 |
| 2 |
∴EF∥AD,EF=AD,
∴四边形AEFD是平行四边形,
∴OF=OA,EO=DO,
又OA=OD,
∴OF=OA=EO=DO,
∴四边形AEFD为矩形.
点评:本题将等腰梯形问题与矩形相结合,在考核学生梯形知识的同时又考查了矩形有关性质,学生在证明四边形为等腰梯形时,常直接找所需条件:同一底上的两底角相等或两条腰相等,而常忽略-关键要素:已经证明该四边形为梯形了吗,故需同学们多加注意.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
参加一次足球联赛的每两个队之间都进行两场比赛,共要比赛110场,共有( )个队参加比赛?
| A、8 | B、9 | C、10 | D、11 |
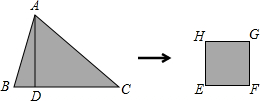 如图,张老师用一张锐角三角形纸板ABC剪出了正方形EFGH,边EF从原BC边上剪下,点H和点G分别在原AB,AC边上,已知BC=18cm,高AD=12cm,则这个正方形纸板的边长是( )
如图,张老师用一张锐角三角形纸板ABC剪出了正方形EFGH,边EF从原BC边上剪下,点H和点G分别在原AB,AC边上,已知BC=18cm,高AD=12cm,则这个正方形纸板的边长是( )| A、6cm | B、6.8cm |
| C、7.2cm | D、9cm |
