Question

12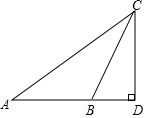．如图，某数学兴趣小组想测量一座塔的高度，他们在广场选择点A处，测得塔顶C的仰角为40°，然后沿着AD的方向前进32m，到达B点，在B处测得塔顶C的仰角为60°．（A、B、D三点在同一条直线上）．请你根据他们的测量数据计算塔CD的高度．（结果精确到整数，参考数据：sin40°≈0.643，cos40°≈0.766，tan40°≈0.839，$\sqrt{3}$=1.732）

Answer 1

分析 在两个直角三角形中用CD表示出AD，BD，列方程解出CD．

解答 解：在Rt△ACD中，∵∠A=40°，
∴AD=$\frac{CD}{tanA}$=$\frac{CD}{0.839}$，
在Rt△BCD中，∵∠CBD=60°，
∴BD=$\frac{\sqrt{3}}{3}$CD，
又AB=AD-BD，
∴$\frac{CD}{0.839}$-$\frac{\sqrt{3}}{3}$CD=32，
解得CD≈55．
答：塔CD的高度是55米．

点评 本题考查仰角的定义，要求学生能借助仰角构造直角三角形并解直角三角形．