题目内容
3.如果一个三角形一边上的中线的长与另两边中点的连线段的长相等,我们称这个三角形为“等线三角形”,这条边称为“等线边”.在等线三角形ABC中,AB为等线边,且AB=3,AC=2,那么BC=$\sqrt{5}$.分析 由三角形的中位线定理证得EF=$\frac{1}{2}$AB,根据题意得出CD=$\frac{1}{2}$AB,从而证得△ABC是直角三角形,再利用勾股定理得出BC的长.
解答 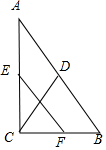 解:∵E,F分别是AC,BC的中点,
解:∵E,F分别是AC,BC的中点,
∴EF=$\frac{1}{2}$AB,
∵CD=EF,
∴CD=$\frac{1}{2}$AB,
∵AD=BD,
∴△ABC是直角三角形,∠ACB=90°,
∵AB=3,AC=2,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{{3}^{2}-{2}^{2}}$=$\sqrt{5}$,
故答案为:$\sqrt{5}$.
点评 此题主要考查了勾股定理的应用,三角形中位线定理,直角三角形的判定,证得是△ABC是直角三角形是解题关键.

练习册系列答案
相关题目
15.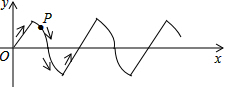 在平面直角坐标系中,若干个半径为1的单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,向右沿这条曲线做上下起伏运动(如图),点P在直线上运动的速度为每秒1个单位长度,点P在弧线上运动的速度为每秒$\frac{π}{3}$个单位长度,则2017秒时,点P的坐标是( )
在平面直角坐标系中,若干个半径为1的单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,向右沿这条曲线做上下起伏运动(如图),点P在直线上运动的速度为每秒1个单位长度,点P在弧线上运动的速度为每秒$\frac{π}{3}$个单位长度,则2017秒时,点P的坐标是( )
 在平面直角坐标系中,若干个半径为1的单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,向右沿这条曲线做上下起伏运动(如图),点P在直线上运动的速度为每秒1个单位长度,点P在弧线上运动的速度为每秒$\frac{π}{3}$个单位长度,则2017秒时,点P的坐标是( )
在平面直角坐标系中,若干个半径为1的单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,向右沿这条曲线做上下起伏运动(如图),点P在直线上运动的速度为每秒1个单位长度,点P在弧线上运动的速度为每秒$\frac{π}{3}$个单位长度,则2017秒时,点P的坐标是( )| A. | ($\frac{2017}{2}$,$\frac{\sqrt{3}}{2}$) | B. | ($\frac{2017}{2}$,-$\frac{\sqrt{3}}{2}$) | C. | (2017,$\sqrt{3}$) | D. | (2017,-$\sqrt{3}$) |
13.下列方程中是一元一次方程的是( )
| A. | x-3=$\frac{1}{2}$ | B. | x2=1 | C. | 2x+y=1 | D. | $\frac{2}{x}-1=0$ |
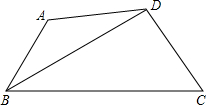 如图,四边形ABCD中,∠A+∠C=180°,BD平分∠ABC,
如图,四边形ABCD中,∠A+∠C=180°,BD平分∠ABC,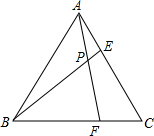 如图,等边△ABC的边长是6,点E,F分别在AC,BC边上,AE=CF,连接AF,BE相交于点P.
如图,等边△ABC的边长是6,点E,F分别在AC,BC边上,AE=CF,连接AF,BE相交于点P.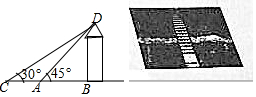 崇圣寺三塔位于大理古城西北部1.5公里处,它是大理历史上规模最为宏大的古刹,南迢丰佑年间曾有殿宇千间,大理国时期是皇家的寺院,崇圣寺三塔由一大二小三阁组成,大塔又名千寻塔.当地群众称它为“文笔塔”,某校数学兴趣小组的同学欲测量主塔垂直于地面的高度BD,他们先在A处测得古塔顶端点D的仰角为45°,再沿着BA的方向后退50.6m至C处,侧得右塔顶端点D的仰角为30°,求该古塔BD的高度($\sqrt{3}≈1.732$,结果保留两位小数).
崇圣寺三塔位于大理古城西北部1.5公里处,它是大理历史上规模最为宏大的古刹,南迢丰佑年间曾有殿宇千间,大理国时期是皇家的寺院,崇圣寺三塔由一大二小三阁组成,大塔又名千寻塔.当地群众称它为“文笔塔”,某校数学兴趣小组的同学欲测量主塔垂直于地面的高度BD,他们先在A处测得古塔顶端点D的仰角为45°,再沿着BA的方向后退50.6m至C处,侧得右塔顶端点D的仰角为30°,求该古塔BD的高度($\sqrt{3}≈1.732$,结果保留两位小数).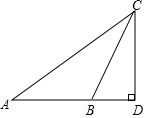 如图,某数学兴趣小组想测量一座塔的高度,他们在广场选择点A处,测得塔顶C的仰角为40°,然后沿着AD的方向前进32m,到达B点,在B处测得塔顶C的仰角为60°.(A、B、D三点在同一条直线上).请你根据他们的测量数据计算塔CD的高度.(结果精确到整数,参考数据:sin40°≈0.643,cos40°≈0.766,tan40°≈0.839,$\sqrt{3}$=1.732)
如图,某数学兴趣小组想测量一座塔的高度,他们在广场选择点A处,测得塔顶C的仰角为40°,然后沿着AD的方向前进32m,到达B点,在B处测得塔顶C的仰角为60°.(A、B、D三点在同一条直线上).请你根据他们的测量数据计算塔CD的高度.(结果精确到整数,参考数据:sin40°≈0.643,cos40°≈0.766,tan40°≈0.839,$\sqrt{3}$=1.732)