题目内容
1. 如图,把矩形ABCD沿EF折叠,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )
如图,把矩形ABCD沿EF折叠,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是( )| A. | 16$\sqrt{3}$ | B. | 24 | C. | 12$\sqrt{3}$ | D. | 12 |
分析 根据翻折变换的特点可求出A′E的长和∠B′FC,进而求出∠A′B′E,根据三角函数求得A′B′的长,从而求出AB的长,根据矩形的面积公式即可得出答案.
解答 解:∵矩形ABCD,
∴∠A=∠B=90°,AD∥BC,
∴∠EB′F=∠B′FC,
有折叠的性质得∠B′FB=∠EFB=60°,A′B′=AB,A′E=AE=2,∠A′B′F=∠B=90,
∴∠EB′F=∠B′FC=60°,
∴∠A′B′E=30°,
∴A′B′=ctan30°=2$\sqrt{3}$,
∴AB=2$\sqrt{3}$,
∵AE=2,DE=6,
∴AD=8,
∴ABCD的面积=AB•AD=2$\sqrt{3}$×8=16$\sqrt{3}$,
故选A.
点评 本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后角相等.

练习册系列答案
相关题目
6.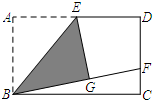 如图,在矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于点F,连接EF,若AB=3,AD=4,则△BCF的周长为( )
如图,在矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于点F,连接EF,若AB=3,AD=4,则△BCF的周长为( )
 如图,在矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于点F,连接EF,若AB=3,AD=4,则△BCF的周长为( )
如图,在矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于点F,连接EF,若AB=3,AD=4,则△BCF的周长为( )| A. | $\frac{13}{3}$ | B. | $\frac{25}{3}$ | C. | 10 | D. | 12 |
13.下列方程中是一元一次方程的是( )
| A. | x-3=$\frac{1}{2}$ | B. | x2=1 | C. | 2x+y=1 | D. | $\frac{2}{x}-1=0$ |
11.在平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2、A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…则正方形A2017B2017C2017D2017的边长是( )


| A. | ($\frac{1}{2}$)2014 | B. | ($\frac{1}{2}$)2015 | C. | ($\frac{\sqrt{3}}{3}$)2016 | D. | ($\frac{\sqrt{3}}{3}$)2017 |
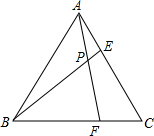 如图,等边△ABC的边长是6,点E,F分别在AC,BC边上,AE=CF,连接AF,BE相交于点P.
如图,等边△ABC的边长是6,点E,F分别在AC,BC边上,AE=CF,连接AF,BE相交于点P.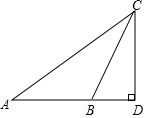 如图,某数学兴趣小组想测量一座塔的高度,他们在广场选择点A处,测得塔顶C的仰角为40°,然后沿着AD的方向前进32m,到达B点,在B处测得塔顶C的仰角为60°.(A、B、D三点在同一条直线上).请你根据他们的测量数据计算塔CD的高度.(结果精确到整数,参考数据:sin40°≈0.643,cos40°≈0.766,tan40°≈0.839,$\sqrt{3}$=1.732)
如图,某数学兴趣小组想测量一座塔的高度,他们在广场选择点A处,测得塔顶C的仰角为40°,然后沿着AD的方向前进32m,到达B点,在B处测得塔顶C的仰角为60°.(A、B、D三点在同一条直线上).请你根据他们的测量数据计算塔CD的高度.(结果精确到整数,参考数据:sin40°≈0.643,cos40°≈0.766,tan40°≈0.839,$\sqrt{3}$=1.732)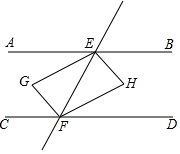 如图,直线AB∥CD,EG平分∠AEF,HE⊥GE于E,且平移EH恰好到GF,则下列结论:①EH平分∠BEF;②EG=HF;③FH平分∠EFD;④∠GFH=90°,其中一定正确的结论有4个.
如图,直线AB∥CD,EG平分∠AEF,HE⊥GE于E,且平移EH恰好到GF,则下列结论:①EH平分∠BEF;②EG=HF;③FH平分∠EFD;④∠GFH=90°,其中一定正确的结论有4个.


