题目内容
18. 如图,PA、PB切⊙O于点A、B,已知⊙O半径为2,且∠APB=60°,则AB=2$\sqrt{3}$.
如图,PA、PB切⊙O于点A、B,已知⊙O半径为2,且∠APB=60°,则AB=2$\sqrt{3}$.
分析 连接PO,AO,根据切线长定理,即可证得PA=PB,则△PAB是等边三角形,在直角△APO中求得AP,即可.
解答 解:连接PO,AO,
∵PA、PB是⊙O的两条切线,切点分别为A、B,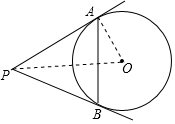
∴PA=PB,
∵∠APB=60°,
∴△PAB是等边三角形,
∵PA、PB切⊙O于点A、B,
∴∠APO=30°,
在直角△APO中,AP=$\frac{OA}{tan30°}$=$\frac{2}{\frac{\sqrt{3}}{3}}$=2$\sqrt{3}$,
∴AB=AP=2$\sqrt{3}$.
故答案为:2$\sqrt{3}$.
点评 本题主要考查了切线长定理,正确证得△PAB是等边三角形是解题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
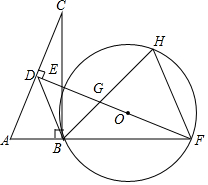 如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,且BF=BC.⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD,FH.
如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,且BF=BC.⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交⊙O于点H,连接BD,FH.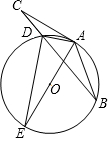 如图,在△ABC中,点D为BC上一点,过A,B,D三点作⊙O,AE是⊙O的直径,AC是⊙O的切线,AD=DC,连结DE.
如图,在△ABC中,点D为BC上一点,过A,B,D三点作⊙O,AE是⊙O的直径,AC是⊙O的切线,AD=DC,连结DE.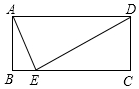 如图,在矩形ABCD中,点E在BC上,连接AE、DE,若AD=DE=2,∠BAE=15°,则CE的长为$\sqrt{3}$.
如图,在矩形ABCD中,点E在BC上,连接AE、DE,若AD=DE=2,∠BAE=15°,则CE的长为$\sqrt{3}$. 如图,在半圆AOB中,半径OA=2,C、D两点在半圆上,若四边形OACD为菱形,则图中阴影部分的面积是2π-2$\sqrt{3}$.
如图,在半圆AOB中,半径OA=2,C、D两点在半圆上,若四边形OACD为菱形,则图中阴影部分的面积是2π-2$\sqrt{3}$.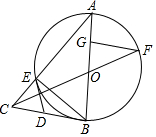 如图,△ABE是⊙O的内接三角形,AB为直径,过点B的切线与AE的延长线交于点C,D是BC的中点,连接DE,连接CO,线段CO的延长线交⊙O于F,FG⊥AB于G.
如图,△ABE是⊙O的内接三角形,AB为直径,过点B的切线与AE的延长线交于点C,D是BC的中点,连接DE,连接CO,线段CO的延长线交⊙O于F,FG⊥AB于G.