题目内容
13.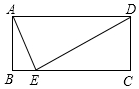 如图,在矩形ABCD中,点E在BC上,连接AE、DE,若AD=DE=2,∠BAE=15°,则CE的长为$\sqrt{3}$.
如图,在矩形ABCD中,点E在BC上,连接AE、DE,若AD=DE=2,∠BAE=15°,则CE的长为$\sqrt{3}$.
分析 只要证明∠ADE=∠EDC=30°,在Rt△DEC中,根据EC=DE•cos30°计算即可.
解答  解:∵四边形ABCD是矩形,
解:∵四边形ABCD是矩形,
∴∠BAD=∠C=90°,AD∥BC,
∵∠BAE=15°,
∴∠DAE=75°,
∵DA=DE,
∴∠DAE=∠DEA=75°,
∴∠ADE=∠EDC=30°,
∴EC=DE•cos30°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
故答案为$\sqrt{3}$.
点评 本题考查矩形的性质、等腰三角形的性质.锐角三角函数等知识,解题的关键是熟练掌握矩形的性质,灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
4.某班的中考英语口语考试成绩如表:
则该班中考英语口语考试成绩的众数比中位数多1分.
| 考试成绩/分 | 30 | 29 | 28 | 27 | 26 |
| 学生数/人 | 3 | 15 | 13 | 6 | 3 |
8.若点A(2,3)在反比例函数y=$\frac{k}{x}$的图象上,则该图象一定经过点( )
| A. | (-2,3) | B. | (1,-6) | C. | (-3,-2) | D. | (3,3) |
 如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到0.1米)
如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到0.1米)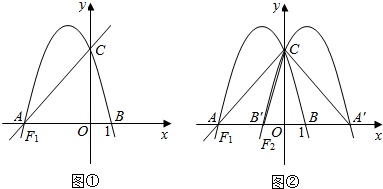
 如图,PA、PB切⊙O于点A、B,已知⊙O半径为2,且∠APB=60°,则AB=2$\sqrt{3}$.
如图,PA、PB切⊙O于点A、B,已知⊙O半径为2,且∠APB=60°,则AB=2$\sqrt{3}$.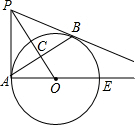 如图,已知点P是⊙O外一点,PB切⊙O于点B,BA 垂直OP于C,交⊙O于点A,连接PA、AO,延长AO,交⊙O于点E.
如图,已知点P是⊙O外一点,PB切⊙O于点B,BA 垂直OP于C,交⊙O于点A,连接PA、AO,延长AO,交⊙O于点E.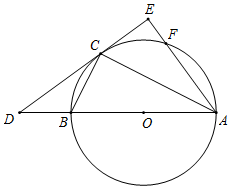 如图,已知△ABC内接于⊙O,AB是⊙O的直径,点F在⊙O上,且满足$\widehat{BC}$=$\widehat{CF}$,过点C作⊙O的切线交AB的延长线于点D,交AF的延长线于点E.
如图,已知△ABC内接于⊙O,AB是⊙O的直径,点F在⊙O上,且满足$\widehat{BC}$=$\widehat{CF}$,过点C作⊙O的切线交AB的延长线于点D,交AF的延长线于点E.