题目内容
3. 如图,在半圆AOB中,半径OA=2,C、D两点在半圆上,若四边形OACD为菱形,则图中阴影部分的面积是2π-2$\sqrt{3}$.
如图,在半圆AOB中,半径OA=2,C、D两点在半圆上,若四边形OACD为菱形,则图中阴影部分的面积是2π-2$\sqrt{3}$.
分析 连接OC,AD,证明△OAC是等边三角形,进而求出AD的长,求出菱形的面积,进而求出阴影部分的面积.
解答 解:连接OC,AD, ∵四边形OACD是菱形,且OA=OC,
∵四边形OACD是菱形,且OA=OC,
∴△OAC是等边三角形,
∵OA=2,
∴OE=1,AE=$\sqrt{3}$,
∴AD=2$\sqrt{3}$,
∴菱形OACD的面积是$\frac{1}{2}$×2×2$\sqrt{3}$=2$\sqrt{3}$,
∴阴影部分的面积是2π-2$\sqrt{3}$,
故答案为2π-2$\sqrt{3}$.
点评 本题主要考查了菱形的性质以及扇形面积的计算,解题的关键是求出菱形的面积.

练习册系列答案
相关题目
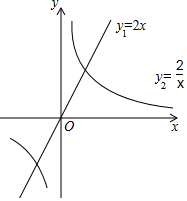 在平面直角坐标系xOy中,直线y1=2x与双曲线y2=$\frac{2}{x}$ 的图象如图所示,小明说:“满足y1>y2的x的取值范围是x>1.”你同意他的观点吗?答:不同意.理由是y1>y2的x的取值范围是x>1或-1<x<0.
在平面直角坐标系xOy中,直线y1=2x与双曲线y2=$\frac{2}{x}$ 的图象如图所示,小明说:“满足y1>y2的x的取值范围是x>1.”你同意他的观点吗?答:不同意.理由是y1>y2的x的取值范围是x>1或-1<x<0. 如图,PA、PB切⊙O于点A、B,已知⊙O半径为2,且∠APB=60°,则AB=2$\sqrt{3}$.
如图,PA、PB切⊙O于点A、B,已知⊙O半径为2,且∠APB=60°,则AB=2$\sqrt{3}$.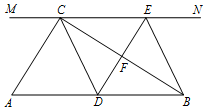 如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上
如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上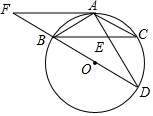 如图,BD为⊙O的直径,AD交BC于点E,AE=2,ED=4,过点A作⊙O的切线FA交DB延长线于点F,且AF∥BC.
如图,BD为⊙O的直径,AD交BC于点E,AE=2,ED=4,过点A作⊙O的切线FA交DB延长线于点F,且AF∥BC.