题目内容
3.(1)阅读下面材料:点 A、B在数轴上分别表示实数a,b,A、B两点之间的距离表示为|AB|,当A、B两点 中有一点在原点时,不妨设点A在原点,如图1所示,|AB|=|BO|=|b|=|a-b|;当A、B两点都不在原点时,①如图2所示,点A、B都在原点的右边,|AB|=|BO|-|OA|=|b|-|a|=b-a=|a-b|; ②如图3所示,点A、B都在原点的左边,|AB|=|BO|-|OA|=|b|-|a|=-b-(-a)=|a-b|;③如图4所示,点A、B在原点的两边多边,|AB|=|BO|+|OA|=|b|+|a|=a+(-b)=|a-b|综上,数轴上A、B两点之间的距离|AB|=|a-b|
回答下列问题:
①数轴上表示2和5的两点之间的距离是3,数轴上表示-2和-5的两点之间的距离是3,数轴上表示1和-3的两点之间的距离是4.
②数轴上表示x和-1的两点A和B之间的距离是|x+1|,如果|AB|=2,那么x为1或-3.
③当代数式|x+1|+|x-2|取最小值时,相应的x的取值范围是-1≤x≤2.
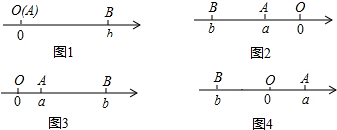
分析 ①②直接根据数轴上A、B两点之间的距离|AB|=|a-b|.代入数值运用绝对值即可求任意两点间的距离.
③根据绝对值的性质,可得到一个一元一次不等式组,通过求解,就可得出x的取值范围.
解答 解:解:①数轴上表示2和5的两点之间的距离是|2-5|=3,数轴上表示-2和-5的两点之间的距离是|-2-(-5)|=3.数轴上表示1和-3的两点之间的距离是|1-(-3)|=4.
故答案为:3,3,4;
②数轴上表示x和-1的两点A和B之间的距离是|x-(-1)|=|x+1|,如果|AB|=2,那么x为1或-3.
故答案为:|x+1|,1或-3;
③当代数式|x+1|十|x-2|取最小值时,
∴x+1≥0,x-2≤0,
∴-1≤x≤2.
故答案为:-1≤x≤2.
点评 此题综合考查了数轴、绝对值的有关内容,用几何方法借助数轴来求解,非常直观,且不容易遗漏,体现了数形结合的优点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.地球上陆地的面积约为148 000 000km2,这个数用科学记数法可以表示为( )
| A. | 148×106km2 | B. | 14.8×107km2 | C. | 1.48×108km2 | D. | 1.48×109km2 |
8.读图填表


| 正方形个数 | 1 | 2 | 3 | 4 | … | n |
| 等腰三角形个数 | 0 | 4 | 8 | 12 | 4n-4 |
 已知数轴:A点表示0,B点表示2,C点表示-1.5.
已知数轴:A点表示0,B点表示2,C点表示-1.5.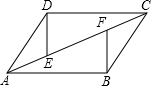 如图,已知AB=CD,BC=DA,E,F是AC上的两点,且AE=CF,试说明DE与BF的关系.
如图,已知AB=CD,BC=DA,E,F是AC上的两点,且AE=CF,试说明DE与BF的关系.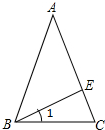 已知:如图,在△ABC中,AB=AC,∠1=$\frac{1}{2}$∠BAC,求证:BE⊥AC.
已知:如图,在△ABC中,AB=AC,∠1=$\frac{1}{2}$∠BAC,求证:BE⊥AC. 如图所示,∠ACB=90°,CD⊥AB,∠1与∠A,∠2与∠B有什么关系?用一个命题表达你所得到的结论为等角的余角相等.
如图所示,∠ACB=90°,CD⊥AB,∠1与∠A,∠2与∠B有什么关系?用一个命题表达你所得到的结论为等角的余角相等.