题目内容
15.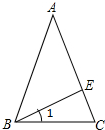 已知:如图,在△ABC中,AB=AC,∠1=$\frac{1}{2}$∠BAC,求证:BE⊥AC.
已知:如图,在△ABC中,AB=AC,∠1=$\frac{1}{2}$∠BAC,求证:BE⊥AC.
分析 过点A作AD⊥BC于点D,根据等腰三角形的性质可知∠CAD=$\frac{1}{2}$∠BAC,故∠1=∠CAD,由直角三角形的性质即可得出结论.
解答  证明:过点A作AD⊥BC于点D,
证明:过点A作AD⊥BC于点D,
∵AB=AC,∠1=$\frac{1}{2}$∠BAC,
∴∠CAD=$\frac{1}{2}$∠BAC,
∴∠1=∠CAD.
∵∠CAD+∠C=90°,
∴∠1+∠C=90°,
∴∠BEC=90°,即BE⊥AC.
点评 本题考查的是等腰三角形的性质,熟知等腰三角形三线合一的性质是解答此题的关键.

练习册系列答案
相关题目
5.下列说法正确的是( )
| A. | 两边和一角对应相等的两三角形全等 | |
| B. | 两边对应相等的两个三角形全等 | |
| C. | 一锐角和一边对应相等的两个直角三角形全等 | |
| D. | 所有的等边三角形都全等 |
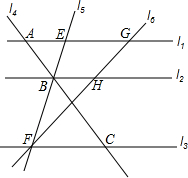 如图,已知,直线l1,l2,l3依次截直线l4于点A、B、C,截直线l5于点E、B、F,截直线l6于点G、H、F,且l1∥l2∥l3,BE=2,BF=4,AB=2.5,FG=9.求BC、FH、GH的长.
如图,已知,直线l1,l2,l3依次截直线l4于点A、B、C,截直线l5于点E、B、F,截直线l6于点G、H、F,且l1∥l2∥l3,BE=2,BF=4,AB=2.5,FG=9.求BC、FH、GH的长.