题目内容
5. 如图,直线a∥b,一块有60°的直角三角尺如图放置,∠1=115°,则∠2=85°.
如图,直线a∥b,一块有60°的直角三角尺如图放置,∠1=115°,则∠2=85°.
分析 根据已知条件和平行线的性质求出∠3的度数,再根据三角形外角性质,求出∠4的度数,从而得出∠2的度数.
解答  解:∵a∥b,
解:∵a∥b,
∴∠1=∠3=115°,
∵∠A=30°,
∴∠4=∠3-∠A=85°,
∵∠2=∠4,
∴∠2=85°,
故答案为:85°.
点评 此题考查了平行线的性质,对顶角相等和三角形外角性质的运用,解题时注意:两直线平行,同位角相等.

练习册系列答案
相关题目
10. 如图,点A,B,C在同一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD、BD于点M、P,CD交BE于点Q,连接PQ,BMM、P,CD交BE于点Q,连接PQ,BM,下面结论:
如图,点A,B,C在同一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD、BD于点M、P,CD交BE于点Q,连接PQ,BMM、P,CD交BE于点Q,连接PQ,BM,下面结论:
①△ABE≌△DBC;
②∠DMA=60°;
③△BPQ为等边三角形;
其中结论正确的有( )
 如图,点A,B,C在同一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD、BD于点M、P,CD交BE于点Q,连接PQ,BMM、P,CD交BE于点Q,连接PQ,BM,下面结论:
如图,点A,B,C在同一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD、BD于点M、P,CD交BE于点Q,连接PQ,BMM、P,CD交BE于点Q,连接PQ,BM,下面结论:①△ABE≌△DBC;
②∠DMA=60°;
③△BPQ为等边三角形;
其中结论正确的有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个. |
14.下列各数中,无理数是( )
| A. | $\sqrt{4}$ | B. | $\frac{π}{2}$ | C. | $\frac{22}{7}$ | D. | 0.16 |
 已知一次函数y=kx+b的图象经过点A(-3,0),B(2,5)两点.正比例函数y=kx的图象经过点B(2,3).
已知一次函数y=kx+b的图象经过点A(-3,0),B(2,5)两点.正比例函数y=kx的图象经过点B(2,3).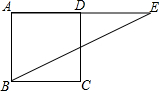 如图,正方形ABCD的边长是3cm,在AD的延长线上有一点E,当BE=$\sqrt{21}$cm时,DE的长是2$\sqrt{3}$-3cm.
如图,正方形ABCD的边长是3cm,在AD的延长线上有一点E,当BE=$\sqrt{21}$cm时,DE的长是2$\sqrt{3}$-3cm.