题目内容
16. 已知一次函数y=kx+b的图象经过点A(-3,0),B(2,5)两点.正比例函数y=kx的图象经过点B(2,3).
已知一次函数y=kx+b的图象经过点A(-3,0),B(2,5)两点.正比例函数y=kx的图象经过点B(2,3).(1)求这两个函数的表达式.
(2)在直角坐标系中,画出这个函数的图象.
(3)求三角形AOB的面积.
分析 (1)将点的坐标代入,运用待定系数法求解;
(2)两点法即可确定函数的图象.
(3)利用A、B点坐标,然后根据面积公式求解即可.
解答 解:(1)∵一次函数y=kx+b的图象经过两点A(-3,0)、B(2,5)
$\left\{\begin{array}{l}{-3k+b=0}\\{2k+b=5}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=3}\end{array}\right.$
所以一次函数的解析式为:y=x+3
∵正比例函数y=kx的图象经过点B(2,5)
∴2k=5 得k=$\frac{5}{2}$
所以正比例函数的解析式为:y=$\frac{5}{2}$x;
(2)函数图象如右图:
(3)∵△AOB的底边OA=3,底边OA上的高为5,
∴△AOB的面积=3×5÷2=7.5.
点评 本题考查待定系数法求函数解析式及三角形的面积的知识,关键是正确得出函数解析式及坐标与线段长度的转化.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
1.二次根式$\sqrt{2-a}$有意义,a的范围是( )
| A. | a>-2 | B. | a<-2 | C. | a=±2 | D. | a≤2 |
8.若不等式组$\left\{\begin{array}{l}{x+8<4x-1}\\{x≥m}\end{array}\right.$的解是x>3,则m的取值范围是( )
| A. | m≥3 | B. | m≤3 | C. | m=3 | D. | m<3 |
6.一次函数y=kx+b 中,y随x的增大而减小,b>0,则这个函数的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
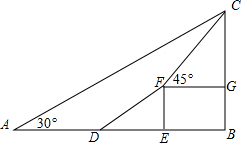 如图,为了测量某建筑物BC的高度,小明先在地面上用测角仪A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了20m到达D处,此时遇到一斜坡,坡度i=1:$\sqrt{3}$,沿着斜坡前进40m到达F处测得建筑物顶部的仰角是45°,(坡度i=1:$\sqrt{3}$是指坡面的铅直高度FE与水平宽度DE的比).
如图,为了测量某建筑物BC的高度,小明先在地面上用测角仪A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了20m到达D处,此时遇到一斜坡,坡度i=1:$\sqrt{3}$,沿着斜坡前进40m到达F处测得建筑物顶部的仰角是45°,(坡度i=1:$\sqrt{3}$是指坡面的铅直高度FE与水平宽度DE的比).
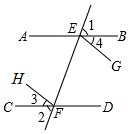 已知,如图,∠1=∠2,∠3=∠4,试说明EG∥FH的道理,以下是说明道理的过程,请将其填写完整,并在括号内填出所得结论的理由.
已知,如图,∠1=∠2,∠3=∠4,试说明EG∥FH的道理,以下是说明道理的过程,请将其填写完整,并在括号内填出所得结论的理由. 如图,直线a∥b,一块有60°的直角三角尺如图放置,∠1=115°,则∠2=85°.
如图,直线a∥b,一块有60°的直角三角尺如图放置,∠1=115°,则∠2=85°.