题目内容
5.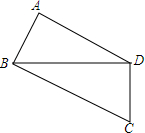 如图,在四边形ABCD中,BA⊥DA,AB=2,AD=2$\sqrt{3}$,CD=3,BC=5,求四边形ABCD的面积.
如图,在四边形ABCD中,BA⊥DA,AB=2,AD=2$\sqrt{3}$,CD=3,BC=5,求四边形ABCD的面积.
分析 先根据勾股定理求出BD的长,再由勾股定理的逆定理判断出△BCD的形状,根据S四边形ABCD=S△ABD+S△BCD即可得出结论.
解答 解:∵BA⊥DA,AB=2,AD=2$\sqrt{3}$,
∴BD=$\sqrt{{AB}^{2}+{AD}^{2}}$=$\sqrt{{2}^{2}+{(2\sqrt{3})}^{2}}$=4.
∵CD=3,BC=5,32+42=52,
∴△BCD是直角三角形,
∴S四边形ABCD=S△ABD+S△BCD=$\frac{1}{2}$AB•AD+$\frac{1}{2}$CD•BD=$\frac{1}{2}$×2×2$\sqrt{3}$+$\frac{1}{2}$×3×4=2$\sqrt{3}$+6.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
15.已知反比例函数y=-$\frac{2}{x}$的图象上有两点A(x1,y1),B(x2,y2),且x1<x2<0,则y1,y2的大小关系为( )
| A. | y1<y2 | B. | y1>y2 | C. | y1=y2 | D. | 无法确定 |
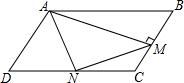 如图,在?ABCD中,N是边DC的中点,AN=3,AM⊥BC交BC于点M,则MN的长是3.
如图,在?ABCD中,N是边DC的中点,AN=3,AM⊥BC交BC于点M,则MN的长是3.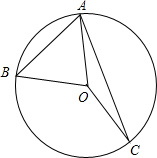 如图,已知点A、B、C在⊙0上,且$\widehat{AB}:\widehat{BC}:\widehat{AC}$=2:3:4.
如图,已知点A、B、C在⊙0上,且$\widehat{AB}:\widehat{BC}:\widehat{AC}$=2:3:4.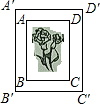 如图是一张矩形照片ABCD,AB:AD=3:2,将它镶嵌在矩形相框A′B′C′D′中,四边留下空隙的宽度相等.试探讨矩形ABCD与矩形A′B′C′D′是否相似,为什么?
如图是一张矩形照片ABCD,AB:AD=3:2,将它镶嵌在矩形相框A′B′C′D′中,四边留下空隙的宽度相等.试探讨矩形ABCD与矩形A′B′C′D′是否相似,为什么? 如图,在△ABC中,AD⊥BC于D,∠BAD=30°,∠C=45°,BD=1.
如图,在△ABC中,AD⊥BC于D,∠BAD=30°,∠C=45°,BD=1. 如图,已知面积为8的正方形ABCD内接于⊙O,求⊙O的内接正六边形AEFCGH的面积.
如图,已知面积为8的正方形ABCD内接于⊙O,求⊙O的内接正六边形AEFCGH的面积.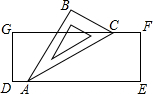 如图,小聪把一块含有30°角的直角三角尺ABC的两个顶点A,C放在长方形纸片DEFG的对边上,若AC平分∠BAE,则∠DAB的度数是120°.
如图,小聪把一块含有30°角的直角三角尺ABC的两个顶点A,C放在长方形纸片DEFG的对边上,若AC平分∠BAE,则∠DAB的度数是120°.