题目内容
13．
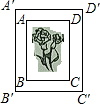如图是一张矩形照片ABCD，AB：AD=3：2，将它镶嵌在矩形相框A′B′C′D′中，四边留下空隙的宽度相等．试探讨矩形ABCD与矩形A′B′C′D′是否相似，为什么？
分析 根据题意设出四边留下空隙的宽度，根据相似多边形的性质列出算式，假设即可．
解答 解：矩形ABCD与矩形A′B′C′D′不相似，
假设矩形ABCD与矩形A′B′C′D′相似，
设四边留下空隙的宽度为x，AB=3y，则AD=2y，
∴$\frac{3y}{2y}$=$\frac{3y-2x}{2y-2x}$，
解得x=0，
故矩形ABCD与矩形A′B′C′D′不相似．
点评 本题考查的是相似多边形的判定，掌握两个多边形的对应角相等，对应边的比相等，则这两个多边形是相似多边形是解题的关键．
练习册系列答案
发散思维新课堂系列答案
相关题目
已知：如图，在△ABC中，AD是高，EF是BC的垂直平分线，EF交AC于E，交BC于F，BE交AD于M．求证：点E在AM的垂直平分线上．
如图，∠AOD=∠BOD=∠COE=90°．找出图中互补和互余的角，和∠BOE相等的角是哪个？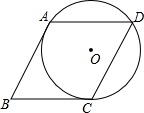
如图，⊙O经过菱形ABCD的三个顶点A，C，D，且与AB相切于点A，求∠ABC的度数．
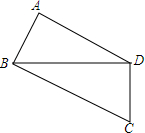如图，在四边形ABCD中，BA⊥DA，AB=2，AD=2$\sqrt{3}$，CD=3，BC=5，求四边形ABCD的面积．