题目内容
10. 如图,已知面积为8的正方形ABCD内接于⊙O,求⊙O的内接正六边形AEFCGH的面积.
如图,已知面积为8的正方形ABCD内接于⊙O,求⊙O的内接正六边形AEFCGH的面积.
分析 连接OC、OD、OG,作OM⊥CG于M,由正方形和正六边形的性质得出CD2=8,△OCD是等腰直角三角形,△COG是等边三角形,得出CD=2$\sqrt{2}$,CG=OC,由勾股定理得出OC═2,OM=$\sqrt{3}$,即可求出正六边形AEFCGH的面积.
解答 解:连接OC、OD、OG,作OM⊥CG于M,如图所示:
根据题意得:CD2=8,△OCD是等腰直角三角形,△COG是等边三角形,
∴CD=2$\sqrt{2}$,CG=OC,
∴OC=$\frac{\sqrt{2}}{2}$CD=2,
∴CG=2,CM=1,
∴OM=$\sqrt{3}$,
∴正六边形AEFCGH的面积=6×$\frac{1}{2}$×2×$\sqrt{3}$=6$\sqrt{3}$.
点评 本题考查了正多边形和圆、正方形的性质、正六边形的性质、等腰直角三角形和等边三角形的判定与性质;熟练掌握正方形和正六边形的性质,由正方形的面积求出圆的半径是解决问题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
19.下列说法中正确的是( )
| A. | 若mx=my,则x=y | B. | 若x=y,则$\frac{x}{{m}^{2}}$=$\frac{y}{{m}^{2}}$ | ||
| C. | 若$\frac{x}{m}$=$\frac{y}{m}$,则x=y | D. | 若x2=y2,则x3=y3 |
20.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  等边三角形 | B. |  等腰梯形 | C. |  平行四边形 | D. |  正方形 |
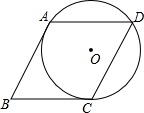 如图,⊙O经过菱形ABCD的三个顶点A,C,D,且与AB相切于点A,求∠ABC的度数.
如图,⊙O经过菱形ABCD的三个顶点A,C,D,且与AB相切于点A,求∠ABC的度数.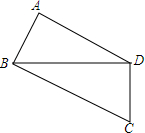 如图,在四边形ABCD中,BA⊥DA,AB=2,AD=2$\sqrt{3}$,CD=3,BC=5,求四边形ABCD的面积.
如图,在四边形ABCD中,BA⊥DA,AB=2,AD=2$\sqrt{3}$,CD=3,BC=5,求四边形ABCD的面积.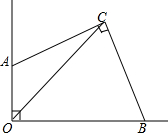 如图,若∠AOB=∠ACB=90°,OC平分∠AOB.
如图,若∠AOB=∠ACB=90°,OC平分∠AOB.