题目内容
5. 如图,在△ABC中,AC=BC,在△ABC外部取一点D,连接AD,BD,CD,且DC平分∠ADB,求证:∠ACB+∠ADB=180°.
如图,在△ABC中,AC=BC,在△ABC外部取一点D,连接AD,BD,CD,且DC平分∠ADB,求证:∠ACB+∠ADB=180°.
分析 如图作CE⊥AD于E,CF⊥DB于F.由Rt△CEA≌Rt△CFB,推出∠ACE=∠CFB,推出ACB=∠ECF,在四边形ECFD中,∠EDF+∠ECF=360°-∠CED-∠CFD=180°,可得∠ACB+∠ADB=180°.
解答  证明:如图作CE⊥AD于E,CF⊥DB于F.
证明:如图作CE⊥AD于E,CF⊥DB于F.
∵CD平分∠ADB,CE⊥AD于E,CF⊥DB于F,
∴CE=CF,∠CEA=∠CFB=90°,
在Rt△CEA和Rt△CFB中,
$\left\{\begin{array}{l}{CA=CB}\\{CE=CF}\end{array}\right.$,
∴Rt△CEA≌Rt△CFB,
∴∠ACE=∠CFB,
∴∠ACB=∠ECF,
在四边形ECFD中,∠EDF+∠ECF=360°-∠CED-∠CFD=180°,
∴∠ACB+∠ADB=180°.
点评 本题考查全等三角形的判定和性质,角平分线的性质定理四边形内角和定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.

练习册系列答案
相关题目
4.若反比例函数y=-$\frac{4}{x}$的图象经过第二象限的点(a,-a),则a的值为( )
| A. | 2或-2 | B. | -2 | C. | 2 | D. | 4 |
17.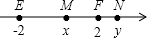 如图,实数-2,2,x,y在数轴上的对应点分别为E、F、M、N,这四个数中绝对值最大的数对应的点是( )
如图,实数-2,2,x,y在数轴上的对应点分别为E、F、M、N,这四个数中绝对值最大的数对应的点是( )
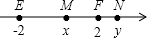 如图,实数-2,2,x,y在数轴上的对应点分别为E、F、M、N,这四个数中绝对值最大的数对应的点是( )
如图,实数-2,2,x,y在数轴上的对应点分别为E、F、M、N,这四个数中绝对值最大的数对应的点是( )| A. | 点E | B. | 点F | C. | 点M | D. | 点N |
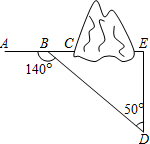 如图,在某隧道建设工程中,需沿AC方向开山修路,为了加快施工进度,要在小山的另一边同时施工,为了使开挖点E在直线AC上,现在AC上取一点B,AC外取一点D,测得∠ABD=140°,BD=704m,∠D=50°,求开挖点E到点D的距离.(结果精确到1米)
如图,在某隧道建设工程中,需沿AC方向开山修路,为了加快施工进度,要在小山的另一边同时施工,为了使开挖点E在直线AC上,现在AC上取一点B,AC外取一点D,测得∠ABD=140°,BD=704m,∠D=50°,求开挖点E到点D的距离.(结果精确到1米) 如图,AB是⊙O的直径,已知AB=2,C,D是⊙O的上的两点,且$\widehat{BC}$+$\widehat{BD}$=$\frac{2}{3}$$\widehat{AB}$,M是AB上一点,则MC+MD的最小值是$\sqrt{3}$.
如图,AB是⊙O的直径,已知AB=2,C,D是⊙O的上的两点,且$\widehat{BC}$+$\widehat{BD}$=$\frac{2}{3}$$\widehat{AB}$,M是AB上一点,则MC+MD的最小值是$\sqrt{3}$.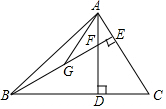 如图,△ABC中,∠ABC=45°,高AD和BE交于F点,点G为BF的中点,AF=4,DF=6,则AG=$\frac{10\sqrt{170}}{17}$.
如图,△ABC中,∠ABC=45°,高AD和BE交于F点,点G为BF的中点,AF=4,DF=6,则AG=$\frac{10\sqrt{170}}{17}$.