题目内容
14. 如图,AB是⊙O的直径,已知AB=2,C,D是⊙O的上的两点,且$\widehat{BC}$+$\widehat{BD}$=$\frac{2}{3}$$\widehat{AB}$,M是AB上一点,则MC+MD的最小值是$\sqrt{3}$.
如图,AB是⊙O的直径,已知AB=2,C,D是⊙O的上的两点,且$\widehat{BC}$+$\widehat{BD}$=$\frac{2}{3}$$\widehat{AB}$,M是AB上一点,则MC+MD的最小值是$\sqrt{3}$.
分析 过D作DD′⊥AB于H交⊙O于D′,根据垂径定理得到$\widehat{BD}$=$\widehat{D′B}$,于是得到∠COD′=120°,连接CD′交AB于M,则CD′=MC+MD的最小值,过O作ON⊥CD′于N,得到CD′=2NC,∠C=30°,解直角三角形得到CN=$\frac{\sqrt{3}}{2}$,即可得到结论.
解答 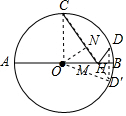 解:过D作DD′⊥AB于H交⊙O于D′,
解:过D作DD′⊥AB于H交⊙O于D′,
∴$\widehat{BD}$=$\widehat{D′B}$,
∵$\widehat{BC}$+$\widehat{BD}$=$\frac{2}{3}$$\widehat{AB}$,
∴$\widehat{BC}$+$\widehat{BD′}$=$\frac{2}{3}$$\widehat{AB}$,
∴∠COD′=120°,
连接CD′交AB于M,
则CD′=MC+MD的最小值,
过O作ON⊥CD′于N,
∵OC=OD′,
∴CD′=2NC,∠C=30°,
∵OC=$\frac{1}{2}$AB=1,
∴CN=$\frac{\sqrt{3}}{2}$,
∴CD′=$\sqrt{3}$,
∴MC+MD的最小值是$\sqrt{3}$,
故答案为:$\sqrt{3}$.
点评 此题考查了垂径定理,勾股定理,以及轴对称-最短线路问题,熟练掌握定理是解本题的关键.

练习册系列答案
相关题目
2.下列说法正确的是( )
| A. | 任何数都有算术平方根 | B. | 只有正数有算术平方根 | ||
| C. | 0和正数都有算术平方根 | D. | 负数有算术平方根 |
9.下列各式中正确的是( )
| A. | ±$\sqrt{9}$=±3 | B. | 16平方根是4 | ||
| C. | (-4)2 的平方根是4 | D. | -(-25)的平方根是-5 |
 如图,扇形AOB中,OA=10,∠AOB=36°,若固定B点,将此扇形按顺时针方向旋转,得一新扇形O′BA′,其中A点在BO′上,则O点旋转至O′点所经过的路径的长度为4π.(结果保留π)
如图,扇形AOB中,OA=10,∠AOB=36°,若固定B点,将此扇形按顺时针方向旋转,得一新扇形O′BA′,其中A点在BO′上,则O点旋转至O′点所经过的路径的长度为4π.(结果保留π) 如图,在△ABC中,AC=BC,在△ABC外部取一点D,连接AD,BD,CD,且DC平分∠ADB,求证:∠ACB+∠ADB=180°.
如图,在△ABC中,AC=BC,在△ABC外部取一点D,连接AD,BD,CD,且DC平分∠ADB,求证:∠ACB+∠ADB=180°.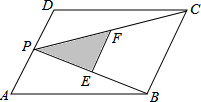 如图,P是平行四边形ABCD边AD上一动点,点E,F分别为PC,PB的中点,对于下列各值:
如图,P是平行四边形ABCD边AD上一动点,点E,F分别为PC,PB的中点,对于下列各值: 如图,已知AB⊥BC,FC⊥BC,AB=BC,点E在BC上,AE⊥BF,垂足为G.求证:AE=BF.
如图,已知AB⊥BC,FC⊥BC,AB=BC,点E在BC上,AE⊥BF,垂足为G.求证:AE=BF.