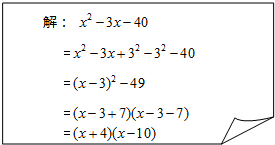题目内容
1. 如图,在等腰Rt△ABC中,∠ABC=90°,O是AC的中点,P,Q分别在AB,BC上(P,Q与A,B,C都不重合),OP⊥OQ,OS⊥AQ交AB于S.下列结论:①BQ=BS;②PA=QB;③S是PB的中点;④$\frac{CQ}{PS}$的值为定值.其中正确结论的个数是( )
如图,在等腰Rt△ABC中,∠ABC=90°,O是AC的中点,P,Q分别在AB,BC上(P,Q与A,B,C都不重合),OP⊥OQ,OS⊥AQ交AB于S.下列结论:①BQ=BS;②PA=QB;③S是PB的中点;④$\frac{CQ}{PS}$的值为定值.其中正确结论的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 由Q是边长BC上的动点,得出①不正确;
由等腰直角三角形的性质和已知条件得出∠OAP=∠BOQ=∠C=∠ABO=∠OBQ=45°,OB=$\frac{1}{2}$AC=OA=OC,∠AOB=90°,证出∠AOP=∠BOQ,由ASA证明△AOP≌△BOQ,得出AP=BQ,OP=OQ,②正确;
过O作OM∥BC,则∠MOQ=∠OQC,证明B,P,O,Q四点共圆,由圆内接四边形的性质得出∠OQC=∠SPO=∠MOQ,证出∠POS=∠OQA,由ASA证明△POS≌△OQM,得出PS=OM,证明OM是△AQE的中位线,得出OM=$\frac{1}{2}$CQ,得出④正确;
同理证出△BOP≌△COQ,得出PB=CQ,得出PS=$\frac{1}{2}$PB,③正确;即可得出结论.
解答 解:∵Q是边长BC上的动点,
∴①不正确;
∵△ABC是等腰直角三角形,∠ABC=90°,O是AC的中点,
∴∠OAP=∠BOQ=∠C=∠ABO=∠OBQ=45°,OB=$\frac{1}{2}$AC=OA=OC,∠AOB=90°,
∵OP⊥OQ,
∴∠POQ=90°,
∴∠AOP=∠BOQ,
在△AOP和△BOQ中,
$\left\{\begin{array}{l}{∠AOP=∠BOQ}&{\;}\\{OA=OB}&{\;}\\{∠OAP=∠OBQ}&{\;}\end{array}\right.$,
∴△AOP≌△BOQ(ASA),
∴AP=BQ,OP=OQ,②正确;
过O作OM∥BC,交AQ于M,如图所示: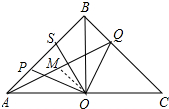
∴∠MOQ=∠OQC,
∵∠ABC=∠POQ=90°,
∴B,P,O,Q四点共圆,
∴∠OQC=∠SPO=∠MOQ,
∵OS⊥AQ,
∴∠OQA+∠QOS=90°,
∵∠POS+∠QOS=90°,
∴∠POS=∠OQA,
在△POS与△OQM中,
$\left\{\begin{array}{l}{∠POS=∠OQA}&{\;}\\{OQ=OP}&{\;}\\{∠MOQ=∠SPO}&{\;}\end{array}\right.$,
∴△POS≌△OQM(ASA),
∴PS=OM,
∵AO=OC,
∴OM是△AQC的中位线,
∴OM=$\frac{1}{2}$CQ,
∴PS=$\frac{1}{2}$CQ,
∴$\frac{CQ}{PS}$=2,④正确;
∵△AOP≌△BOQ,同理:△BOP≌△COQ,
∴PB=CQ,
∴PS=$\frac{1}{2}$PB,
即S是PB的中点,③正确;
正确结论的个数有3个.
故选:C.
点评 本题考查了等腰直角三角形的性质、全等三角形的判定与性质、三角形中位线定理、四点共圆、圆内接四边形的性质、平行线的性质等知识;本题综合性强,难度较大,证明三角形全等是解决问题的关键.

①长方体;②三棱柱;③圆锥;④圆柱.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
列代数式:比x的2倍少4的数记作A,则A=2x-4
比$\frac{1}{2}x$的相反数多2的数记作B,则B=$-\frac{1}{2}x+2$.
(1)根据所给x的值求上述代数式的值并填入表格:
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| A | … | … | |||||
| B | … | … |
(3)若A和B的值相差3,求x的值.
 某蔬菜基地要把一批新鲜蔬菜运往外地,有两种运输方式可供选择,主要参看数据如下:
某蔬菜基地要把一批新鲜蔬菜运往外地,有两种运输方式可供选择,主要参看数据如下:| 运输方式 | 运输速度(km/h) | 装卸费用(元) | 途中综合费用(元/h) |
| 汽车 | m | 200 | 270 |
| 火车 | 100 | n | 240 |
(1)求m,n及y1,y2的表达式;
(2)考虑到运用汽车运输方便,只有汽车途中用时比火车的途中用时多用2小时以上(含2小时),才选用火车运输,问此时运用火车运输比用汽车运输至少节省多少元?
| A. | -(-3) | B. | |-3| | C. | 3×(-2)2 | D. | -32 |