题目内容
11.如图,用同样规格的黑白两色正方形瓷砖铺设矩形地面,请观察下列图形,探究下列问题,并直接写出结果.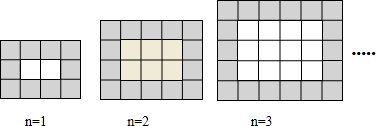
(1)在第4个图中,共有白色瓷砖20块;在第n个图中,共有白色瓷砖n2+n块;
(2)在第4个图中,共有瓷砖42块;在第n个图中,共有瓷砖(n+3)(n+2)块.
分析 (1)通过观察发现规律,得出在第n个图形中,白瓷砖的块数,然后将n=4代入即可;
(2)将黑色瓷砖和白色瓷砖加在一起即可得到答案;
解答 解:(1)通过观察图形可知,当n=1时,用白瓷砖2块,黑瓷砖10块;
当n=2时,用白瓷砖6块,黑瓷砖14块;
当n=3时,用白瓷砖12块,黑瓷砖18块;
可以发现,需要白瓷砖的数量和图形数之间存在这样的关系,即白瓷砖块数等于图形数的平方加上图形数;
需要黑瓷砖的数量和图形数之间存在这样的关系,即黑瓷砖块数等于图形数的4倍加上图形数.
所以,在第n个图形中,白瓷砖的块数可用含n的代数式表示为n2+n;
黑瓷砖的块数可用含n的代数式表示为4n+6.
当n=4时,白色瓷砖有n2+n=16+4=20(块),
故答案为:20;n2+n;
(2)由(1)可得总块数可表示为n2+n+4n+6=(n+3)(n+2),
在第4个图中,共有瓷砖42;
故答案为:42;(n+2)(n+3).
点评 此题主要考查学生对图形变化类这个知识点的理解和掌握,此题有一定拔高难度,属于难题,解答此题的关键是通过观察和分析,找出其中的规律.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1. 如图,在等腰Rt△ABC中,∠ABC=90°,O是AC的中点,P,Q分别在AB,BC上(P,Q与A,B,C都不重合),OP⊥OQ,OS⊥AQ交AB于S.下列结论:①BQ=BS;②PA=QB;③S是PB的中点;④$\frac{CQ}{PS}$的值为定值.其中正确结论的个数是( )
如图,在等腰Rt△ABC中,∠ABC=90°,O是AC的中点,P,Q分别在AB,BC上(P,Q与A,B,C都不重合),OP⊥OQ,OS⊥AQ交AB于S.下列结论:①BQ=BS;②PA=QB;③S是PB的中点;④$\frac{CQ}{PS}$的值为定值.其中正确结论的个数是( )
 如图,在等腰Rt△ABC中,∠ABC=90°,O是AC的中点,P,Q分别在AB,BC上(P,Q与A,B,C都不重合),OP⊥OQ,OS⊥AQ交AB于S.下列结论:①BQ=BS;②PA=QB;③S是PB的中点;④$\frac{CQ}{PS}$的值为定值.其中正确结论的个数是( )
如图,在等腰Rt△ABC中,∠ABC=90°,O是AC的中点,P,Q分别在AB,BC上(P,Q与A,B,C都不重合),OP⊥OQ,OS⊥AQ交AB于S.下列结论:①BQ=BS;②PA=QB;③S是PB的中点;④$\frac{CQ}{PS}$的值为定值.其中正确结论的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.线段2cm、8cm的比例中项为( )cm.
| A. | 4 | B. | 8 | C. | ±4 | D. | ±8 |
20.2015年,号称“千湖之省”的湖北正遭受大旱,为提高学生的环保意识,节约用水,某校数学教师编造了一道应用题:为了保护水资源,某市制定一套节水的管理措施,其中对居民生活用水的收费作如下规定:
如某居民一月份用水9吨,则应收水费为:6×2+4×(9-6)=24(元)
(1)若该户居民3月份用水13吨,则应收水费52 元.
(2)若该户居民5、6月份共用水15吨(五月份用水超过六月份),共交水费44元,则该户居民5、6月份各用水多少吨?
| 月用水量(单位:吨) | 单价(单位:元/吨) |
| 不大于6吨部分 | 2 |
| 大于6吨且不大于10吨部分 | 4 |
| 大于10吨部分 | 8 |
(1)若该户居民3月份用水13吨,则应收水费52 元.
(2)若该户居民5、6月份共用水15吨(五月份用水超过六月份),共交水费44元,则该户居民5、6月份各用水多少吨?
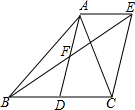 如图,AD是△ABC的中线,AE∥BC,BE交AD于点F,且AF=DF.
如图,AD是△ABC的中线,AE∥BC,BE交AD于点F,且AF=DF. 如图,E、F为线段AB上两点,AD∥CB,且AD=CB,∠D=∠C.求证:AF=BE.
如图,E、F为线段AB上两点,AD∥CB,且AD=CB,∠D=∠C.求证:AF=BE.