题目内容
13.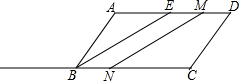 如图,在平行四边形ABCD中,AD=2AB=6cm,BE是∠ABC的角平分线,点M从点E出发,沿ED方向以1cm/s的速度向点D运动,点N从点C出发,沿射线CB方向运动,以4cm/s的运动速度,当点M运动到点D时,点N随之停止运动,设运动时间为t秒.
如图,在平行四边形ABCD中,AD=2AB=6cm,BE是∠ABC的角平分线,点M从点E出发,沿ED方向以1cm/s的速度向点D运动,点N从点C出发,沿射线CB方向运动,以4cm/s的运动速度,当点M运动到点D时,点N随之停止运动,设运动时间为t秒.(1)求AE的长;
(2)是否存在以M、E、B、N为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,请说明理由.
(3)当t=1时,线段NM将平行四边形ABCD面积二等分(直接写出答案).
分析 (1)利用平行四边形的性质得出∠AEB=∠CBE,再利用角平分线的定义得出∠ABE=∠CBE即可得出结论;
(2)利用平行四边形的性质即可得出EM=BN,再分两种情况讨论计算即可得出结论;
(3)利用平行四边形的性质经过平行四边形的中心的直线将平行四边形的面积二等分,再建立方程即可得出结论.
解答 解:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠AEB=∠CBE,
∵BE是∠ABC的角平分线,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AE=AB,
∵2AB=6cm,
∴AE=3cm;
(2)由(1)知,AE=3,
∵AD=6,
∴DE=AD-AB=3,
由运动知,EM=t,CN=4t(0≤t≤3),
∵AD∥BC,要以M、E、B、N为顶点的四边形是平行四边形,只要EM=BN,
当点N在边BC上时,EN=BC-CN=6-4t,
∴t=6-4t,
∴t=$\frac{6}{5}$
当点N在边CB的延长线上时,EN=CN-BC=4t-6,
∴t=4t-6,
∴t=2,
∴t=$\frac{6}{5}$或t=2时,以M、E、B、N为顶点的四边形是平行四边形;
(3)如图,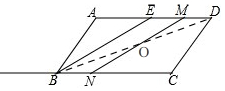
连接BD交MN于O,
∵线段NM将平行四边形ABCD面积二等分,
∴MN必过BD的中点,
∴OB=OD,
∵AD∥BC,
∴∠MDO=∠NBO,
在△MOD和△NOB中,$\left\{\begin{array}{l}{∠MDO=∠NBO}\\{OD=OB}\\{∠DOM=BON}\end{array}\right.$,
∴△MOD≌△NOB,
∴DM=BN,
由运动知,EM=t,CN=4t,
∴DM=3-t,BN=6-4t,
∴3-t=6-4t,
∴t=1,
∴t=1时,线段MN将平行四边形ABCD面积二等分,
故答案为1.
点评 此题是四边形的综合题,主要考查了平行四边形的性质和判定,全等三角形的判定和性质,角平分线的定义;解(1)的关键是得出∠ABE=∠AEB,解(2)的关键是分类讨论的思想建立方程求解,解(3)的关键是判断出OB=OD.

 小亮家与姥姥家相距24km,小亮8:00从家出发,骑自行车去姥姥家,妈妈8:30从家出发,乘车沿相同路线去姥姥家.在同一直角坐标系中,小亮和妈妈的行进路程S(km)与北京时间t(时)的函数图象如图所示.根据图象得到小亮结论,其中错误的是( )
小亮家与姥姥家相距24km,小亮8:00从家出发,骑自行车去姥姥家,妈妈8:30从家出发,乘车沿相同路线去姥姥家.在同一直角坐标系中,小亮和妈妈的行进路程S(km)与北京时间t(时)的函数图象如图所示.根据图象得到小亮结论,其中错误的是( )| A. | 小亮骑自行车的平均速度是12km/h | |
| B. | 妈妈比小亮提前0.5小时到达姥姥家 | |
| C. | 9:00妈妈追上小亮 | |
| D. | 妈妈在距家13km处追上小亮 |
| A. |  | B. |  | C. |  | D. |  |

 正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按如图所示的方式放置,点A1,A2,A3,…和点C1,C2,C3,…,分别在直线y=kx+b(k>0)和x轴上,已知点B1、B2的坐标分别为B1(1,1)、B2(3,2),则B6的坐标是(63,32).
正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按如图所示的方式放置,点A1,A2,A3,…和点C1,C2,C3,…,分别在直线y=kx+b(k>0)和x轴上,已知点B1、B2的坐标分别为B1(1,1)、B2(3,2),则B6的坐标是(63,32). 如图,∠BDC=150°,∠B=$\frac{1}{3}$∠BDC,∠C=28°,则∠A的度数为70°.
如图,∠BDC=150°,∠B=$\frac{1}{3}$∠BDC,∠C=28°,则∠A的度数为70°.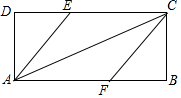 矩形ABCD中,点E、F分别在边CD、AB上,且DE=BF.∠ECA=∠FCA.
矩形ABCD中,点E、F分别在边CD、AB上,且DE=BF.∠ECA=∠FCA.