题目内容
8. 正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按如图所示的方式放置,点A1,A2,A3,…和点C1,C2,C3,…,分别在直线y=kx+b(k>0)和x轴上,已知点B1、B2的坐标分别为B1(1,1)、B2(3,2),则B6的坐标是(63,32).
正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按如图所示的方式放置,点A1,A2,A3,…和点C1,C2,C3,…,分别在直线y=kx+b(k>0)和x轴上,已知点B1、B2的坐标分别为B1(1,1)、B2(3,2),则B6的坐标是(63,32).
分析 根据题意可求出点A1与A2的坐标,然后求出直线的解析式,然后求出A1、A2、A3的坐标,找出其中的规律即可求出B6的坐标.
解答 解:由题意可知:A1(0,1),A2(1,2)
∴将(0,1)与(1,2)代入y=kx+b,
∴$\left\{\begin{array}{l}{1=b}\\{2=k+b}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$
∴直线的解析式为:y=x+1,
∴A1(0,1),A2(1,2),A3(3,4),A4(7,8),
∴An的纵坐标为:2n-1,
∴An的横坐标为:2n-1-1,
∴An-1的坐标为:(2n-2-1,2n-2)
∴Bn-1的坐标为:(2n-1-1,2n-2),
∴当n=7时,
∴B6=(26-1,25),
即(63,32)
故答案为:(63,32)
点评 本题考查规律型问题,解题的关键是根据题意找出规律,本题属于中等题型.

练习册系列答案
相关题目
19.已知□×(-$\frac{1}{2017}$)=-1,则□等于( )
| A. | $\frac{1}{2017}$ | B. | 2016 | C. | 2017 | D. | 2018 |
5.从有关方面获悉,从今年开始,在我市新成立的两江新区的广大农村准备实行农村新型合作医疗保险制度,享受医保的农民可在规定的医院就医并按照规定标准报销部分医疗费用.如表是医疗费用报销的标准:
(说明:住院医疗费用的报销分段计算,如:某人住院医疗费用共30000元,则4000元按40%报销,16000元按a%报销,余下的10000元按60%报销,题中涉及到的医疗费均指允许报销的医疗费)
(1)某农民在2010年门诊看病自己共支付医疗费270元,则他在这一年中门诊医疗费用450元;
(2)已知农民张大爷一年中住院的实际医疗费用为18000元,按标准可报销7900元,求a的值;
(3)若某农民一年中住院的实际医疗费用为x元(4001≤x≤20000),按标准报销的金额为y元,试用x的式子表示y;
(4)若李大叔一年内本人自负住院费18400元(自付医疗费=实际医疗费-按标准报销的金额),则李大叔这一年实际医疗费用共多少?
| 医疗费用 | 门诊 | 住院 | ||
| 0-4000元 | 4001-20000元 | 20000以上 | ||
| 每年报销比例标准 | 40% | 40% | a% | 60% |
(1)某农民在2010年门诊看病自己共支付医疗费270元,则他在这一年中门诊医疗费用450元;
(2)已知农民张大爷一年中住院的实际医疗费用为18000元,按标准可报销7900元,求a的值;
(3)若某农民一年中住院的实际医疗费用为x元(4001≤x≤20000),按标准报销的金额为y元,试用x的式子表示y;
(4)若李大叔一年内本人自负住院费18400元(自付医疗费=实际医疗费-按标准报销的金额),则李大叔这一年实际医疗费用共多少?
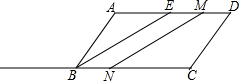 如图,在平行四边形ABCD中,AD=2AB=6cm,BE是∠ABC的角平分线,点M从点E出发,沿ED方向以1cm/s的速度向点D运动,点N从点C出发,沿射线CB方向运动,以4cm/s的运动速度,当点M运动到点D时,点N随之停止运动,设运动时间为t秒.
如图,在平行四边形ABCD中,AD=2AB=6cm,BE是∠ABC的角平分线,点M从点E出发,沿ED方向以1cm/s的速度向点D运动,点N从点C出发,沿射线CB方向运动,以4cm/s的运动速度,当点M运动到点D时,点N随之停止运动,设运动时间为t秒.