题目内容
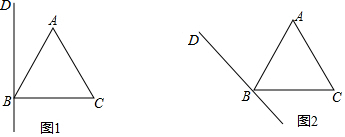
3．
如图，∠BDC=150°，∠B=$\frac{1}{3}$∠BDC，∠C=28°，则∠A的度数为70°．
分析 延长BD交AC于E，根据已知条件和平角的定义得到∠B=50°，∠CED=180°-150°=30°，由三角形的外角的性质得到∠AEB=∠C+∠CDE=60°，根据三角形的内角和即可得到结论．
解答 
解：延长BD交AC于E，
∵∠BDC=150°，∠B=$\frac{1}{3}$∠BDC，
∴∠B=50°，∠CED=180°-150°=30°，
∴∠AEB=∠C+∠CDE=60°，
∴∠A=180°-∠B-∠AED=70°．
故答案为：70°．
点评 本题考查了三角形的内角和，三角形的情景的性质，熟练掌握三角形的内角和是解题的关键．
练习册系列答案
相关题目
8．
如图，在菱形ABCD中，DE⊥AB，cosA=$\frac{3}{5}$，BE=3，则tan∠DBE的值是（ ）
如图，在菱形ABCD中，DE⊥AB，cosA=$\frac{3}{5}$，BE=3，则tan∠DBE的值是（ ）| A． | $\frac{4}{3}$ | B． | 2 | C． | $\frac{\sqrt{5}}{2}$ | D． | $\frac{\sqrt{5}}{5}$ |
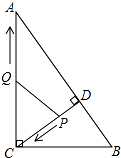如图，在Rt△ABC中，∠ACB=90°，AC=8，BC=6，CD⊥AB于点D，点P从点D出发，沿线段DC向点C运动，点Q从点C出发，沿线段CA向点A运动，两点同时出发，速度都为每秒1个单位长度，当点P运动到C时，两点都停止．设运动时间为t秒．
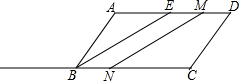如图，在平行四边形ABCD中，AD=2AB=6cm，BE是∠ABC的角平分线，点M从点E出发，沿ED方向以1cm/s的速度向点D运动，点N从点C出发，沿射线CB方向运动，以4cm/s的运动速度，当点M运动到点D时，点N随之停止运动，设运动时间为t秒．
在矩形ABCD中，AB=6，AD=8，P是BC边上一个动点（不与点B重合）．设PA=x，点D到PA的距离为y，求y与x之间的函数表达式，并求出自变量x的取值范围．
