题目内容
11. 如图,已知△ABC的内切圆⊙O,若∠DEF=54°,则∠BAC等于72°.
如图,已知△ABC的内切圆⊙O,若∠DEF=54°,则∠BAC等于72°.
分析 连接OD、OF;根据切线的性质知:OD⊥AB,OF⊥AC,则四边形ADOF中,∠A+∠DOF=180°;那么解题的关键是求出∠DOF的度数,在⊙O中,∠DOF和∠DEF是同弧所对的圆心角和圆周角,根据圆周角定理,易求得∠DOF的度数,由此得解.
解答 解:如图,连接OD、OE,则∠ODA=∠OFA=90°;
⊙O中,∠DOF=2∠DEF=2×54°=108°;
四边形ADEF中,∠ODA=∠OFA=90°,
∴∠BAC+∠DOF=180°,
即∠BAC=180°-∠DOF=72°.
故答案为72°.
点评 本题主要考查了三角形的内切圆与内心的知识,解答本题的关键正确作出辅助线证明出∠DOF=108°,此题难度不大.

练习册系列答案
相关题目
1.算式(2+1)•(22+1)•(24+1)…(232+1)+1计算结果的个位数字是( )
| A. | 4 | B. | 6 | C. | 2 | D. | 8 |
16. 如图,AB∥CD,下列结论中错误的是( )
如图,AB∥CD,下列结论中错误的是( )
 如图,AB∥CD,下列结论中错误的是( )
如图,AB∥CD,下列结论中错误的是( )| A. | ∠1=∠2 | B. | ∠2+∠5=180° | C. | ∠2+∠3=180° | D. | ∠3+∠4=180° |

 如图,O为直线AB上的一点,且∠AOC=$\frac{1}{2}$∠BOC,则∠BOC的度数是120°.
如图,O为直线AB上的一点,且∠AOC=$\frac{1}{2}$∠BOC,则∠BOC的度数是120°.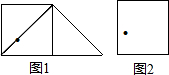 如图,正方形的对角线上有一个小孔,经过小孔剪一刀(不剪曲线和折线)可以将剪下的两片拼成一个三角形,拼成的三角形内部没有小孔,如图1;图2中的正方形中也有一个小孔,但它不在对角线上,将它剪成三片,用剪成的三片拼成一个三角形,要求拼成的三角形内部没有小孔.仿照图1把剪切线和拼成的三角形画出来.
如图,正方形的对角线上有一个小孔,经过小孔剪一刀(不剪曲线和折线)可以将剪下的两片拼成一个三角形,拼成的三角形内部没有小孔,如图1;图2中的正方形中也有一个小孔,但它不在对角线上,将它剪成三片,用剪成的三片拼成一个三角形,要求拼成的三角形内部没有小孔.仿照图1把剪切线和拼成的三角形画出来.