题目内容
3.八年级(3)班开展班队活动,准备用32元钱购买笔记本和中性笔两种奖品,已知笔记本6元/本,中性笔2元/支,且每种奖品至少买1件.(1)若设购买笔记本x本,中性笔y支,试写出y与x之间的关系式;
(2)有多少种购买方案?请列举所有可能的结果;
(3)从上述方案中任选一种方案购买,求买到的中性笔与笔记本数量相等的概率.
分析 (1)首先由题意可得:6x+2y=32,继而求得y与x之间的关系式;
(2)根据每种奖品至少买1件,即可求得所有可能的结果;
(3)由买到的中性笔与笔记本数量相等的只有1种情况,直接利用概率公式求解即可求得答案.
解答 解:(1)根据题意得:6x+2y=32,
∴y=16-3x;
(2)购买方案:x=1,y=13;
x=2,y=10; x=3,y=7;
x=4,y=4; x=5,y=1;
∴共有5种购买方案.
(3)∵买到的中性笔与笔记本数量相等的只有1种情况,
∴P(买到的中性笔与笔记本数量相等)=$\frac{1}{5}$.
点评 本题考查了列举法求概率的知识.注意用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目
18.给出下面四个命题:
(1)全等三角形是相似三角形
(2)顶角相等的两个等腰三角形是相似三角形
(3)所有的等边三角形都相似
(4)有一组对边平行,另一组对边相等的四边形一定是等腰梯形.
其中真命题的个数有( )
(1)全等三角形是相似三角形
(2)顶角相等的两个等腰三角形是相似三角形
(3)所有的等边三角形都相似
(4)有一组对边平行,另一组对边相等的四边形一定是等腰梯形.
其中真命题的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.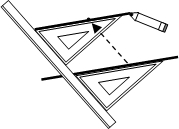 如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
 如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )| A. | 两直线平行,同位角相等 | B. | 内错角相等,两直线平行 | ||
| C. | 同旁内角互补,两直线平行 | D. | 同位角相等,两直线平行 |
12.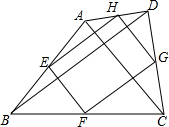 如图,顺次连接四边形ABCD各边的中点,若得到的四边形EFCH为矩形,则四边形ABCD一定满足( )
如图,顺次连接四边形ABCD各边的中点,若得到的四边形EFCH为矩形,则四边形ABCD一定满足( )
 如图,顺次连接四边形ABCD各边的中点,若得到的四边形EFCH为矩形,则四边形ABCD一定满足( )
如图,顺次连接四边形ABCD各边的中点,若得到的四边形EFCH为矩形,则四边形ABCD一定满足( )| A. | AC⊥BD | B. | AD∥BC | C. | AC=BD | D. | AB=CD |
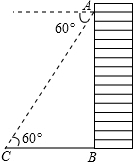 已知在离地面30米的高楼窗台A处测得地面花坛中心标志物C的俯角为60°,那么这一标志物C离此栋楼房的地面距离BC为10$\sqrt{3}$米.
已知在离地面30米的高楼窗台A处测得地面花坛中心标志物C的俯角为60°,那么这一标志物C离此栋楼房的地面距离BC为10$\sqrt{3}$米. 如图,已知△ABC的内切圆⊙O,若∠DEF=54°,则∠BAC等于72°.
如图,已知△ABC的内切圆⊙O,若∠DEF=54°,则∠BAC等于72°. 如图,∠1=121°,∠2=120°,∠3=120°,试写出其中的平行线,并说明理由.
如图,∠1=121°,∠2=120°,∠3=120°,试写出其中的平行线,并说明理由.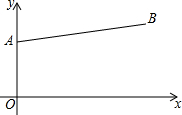 已知:如图,点A(0,6),点B(14,8),在第四象限找点C,使得△ABC为等腰三角形,且∠C=45°,则点C的坐标为(2,-8)、(8+$\sqrt{2}$,-7$\sqrt{2}$)、(16,-6).
已知:如图,点A(0,6),点B(14,8),在第四象限找点C,使得△ABC为等腰三角形,且∠C=45°,则点C的坐标为(2,-8)、(8+$\sqrt{2}$,-7$\sqrt{2}$)、(16,-6).