题目内容
1.算式(2+1)•(22+1)•(24+1)…(232+1)+1计算结果的个位数字是( )| A. | 4 | B. | 6 | C. | 2 | D. | 8 |
分析 原式变形后,利用平方差公式计算得到结果,归纳总结即可确定出结果的个位数字.
解答 解:原式=(2-1)•(2+1)•(22+1)•(24+1)…(232+1)+1
=(22-1)•(22+1)•(24+1)…(232+1)+1
=(24-1)•(24+1)…(232+1)+1
=264-1+1
=264,
∵21=2,22=4,23=8,24=16,25=32,…,
∴其结果个位数以2,4,8,6循环,
∵64÷4=16,
∴原式计算结果的个位数字为6.
故选B
点评 此题考查了平方差公式,熟练掌握平方差公式是解本题的关键.

练习册系列答案
相关题目
11.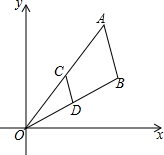 如图,线段AB两个端点的坐标分别为A(6,8),B(7,4),以原点为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD.则端点C的坐标为( )
如图,线段AB两个端点的坐标分别为A(6,8),B(7,4),以原点为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD.则端点C的坐标为( )
 如图,线段AB两个端点的坐标分别为A(6,8),B(7,4),以原点为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD.则端点C的坐标为( )
如图,线段AB两个端点的坐标分别为A(6,8),B(7,4),以原点为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD.则端点C的坐标为( )| A. | (3,3) | B. | (4,3) | C. | (3,4) | D. | ($\frac{7}{2}$,2) |
12.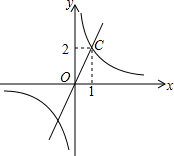 反比例函数y﹦$\frac{k}{x}$和正比例函数y﹦mx的图象如图所示.由此可以得到方程$\frac{k}{x}$﹦mx的实数根为( )
反比例函数y﹦$\frac{k}{x}$和正比例函数y﹦mx的图象如图所示.由此可以得到方程$\frac{k}{x}$﹦mx的实数根为( )
 反比例函数y﹦$\frac{k}{x}$和正比例函数y﹦mx的图象如图所示.由此可以得到方程$\frac{k}{x}$﹦mx的实数根为( )
反比例函数y﹦$\frac{k}{x}$和正比例函数y﹦mx的图象如图所示.由此可以得到方程$\frac{k}{x}$﹦mx的实数根为( )| A. | x=1 | B. | x=2 | C. | x1=1,x2=-1 | D. | x1=1,x2=-2 |
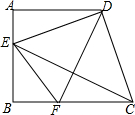 如图,已知在梯形ABCD中,AD∥BC,∠A=90°,AB=AD,点E在边AB上,且DE⊥CD,DF平分∠EDC,交BC于点F,联结CE、EF.
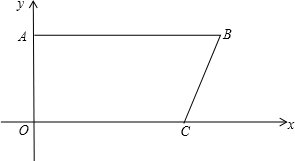
如图,已知在梯形ABCD中,AD∥BC,∠A=90°,AB=AD,点E在边AB上,且DE⊥CD,DF平分∠EDC,交BC于点F,联结CE、EF.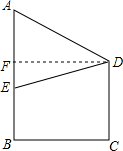 如图,某地为响应市政府“形象重于生命”的号召,在甲建筑物上从点A到点E挂一长为30米的宣传条幅,在乙建筑物的顶部D点测得条幅顶端A点的仰角为40°,测得条幅底端E的俯角为26°,求甲、乙两建筑物的水平距离BC的长(精确到0.1米).
如图,某地为响应市政府“形象重于生命”的号召,在甲建筑物上从点A到点E挂一长为30米的宣传条幅,在乙建筑物的顶部D点测得条幅顶端A点的仰角为40°,测得条幅底端E的俯角为26°,求甲、乙两建筑物的水平距离BC的长(精确到0.1米).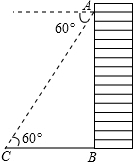 已知在离地面30米的高楼窗台A处测得地面花坛中心标志物C的俯角为60°,那么这一标志物C离此栋楼房的地面距离BC为10$\sqrt{3}$米.
已知在离地面30米的高楼窗台A处测得地面花坛中心标志物C的俯角为60°,那么这一标志物C离此栋楼房的地面距离BC为10$\sqrt{3}$米. 如图,已知△ABC的内切圆⊙O,若∠DEF=54°,则∠BAC等于72°.
如图,已知△ABC的内切圆⊙O,若∠DEF=54°,则∠BAC等于72°.