题目内容
1．
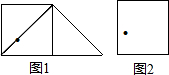如图，正方形的对角线上有一个小孔，经过小孔剪一刀（不剪曲线和折线）可以将剪下的两片拼成一个三角形，拼成的三角形内部没有小孔，如图1；图2中的正方形中也有一个小孔，但它不在对角线上，将它剪成三片，用剪成的三片拼成一个三角形，要求拼成的三角形内部没有小孔．仿照图1把剪切线和拼成的三角形画出来．
分析 沿AB、CD中点剪开，使BW=AN，NC=DF利用全等三角形的性质即可得出答案．
解答 解：如图所示：
点评 此题主要考查了图形的剪拼，利用全等三角形的性质得出是解题关键．
练习册系列答案
相关题目
如图，已知△ABC的内切圆⊙O，若∠DEF=54°，则∠BAC等于72°．
12．
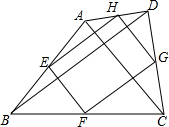如图，顺次连接四边形ABCD各边的中点，若得到的四边形EFCH为矩形，则四边形ABCD一定满足（ ）
如图，顺次连接四边形ABCD各边的中点，若得到的四边形EFCH为矩形，则四边形ABCD一定满足（ ）| A． | AC⊥BD | B． | AD∥BC | C． | AC=BD | D． | AB=CD |
9．
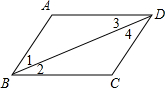在如图中，下列能判定AD∥BC是（ ）
在如图中，下列能判定AD∥BC是（ ）| A． | ∠1=∠2 | B． | ∠3=∠4 | C． | ∠2=∠3 | D． | ∠1=∠4 |
16．
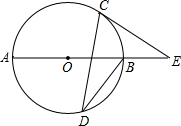如图，AB是⊙O的直径，C，D 是⊙O上的点，∠CDB=30°，过点C作⊙O的切线交AB的延长线于E，则sinE的值为（ ）
如图，AB是⊙O的直径，C，D 是⊙O上的点，∠CDB=30°，过点C作⊙O的切线交AB的延长线于E，则sinE的值为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{\sqrt{3}}{3}$ |
如图，点D、E、F分别在△ABC的三边上，DE∥AC，DF∥AB，已知∠1=55°，则∠2=55°．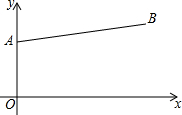
已知：如图，点A（0，6），点B（14，8），在第四象限找点C，使得△ABC为等腰三角形，且∠C=45°，则点C的坐标为（2，-8）、（8+$\sqrt{2}$，-7$\sqrt{2}$）、（16，-6）．
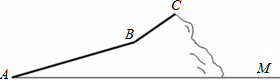数学活动小组组织一次登山活动，他们从山脚下A点出发沿斜坡AB到达B点，再从B点沿斜坡BC到达山顶C点，路线如图所示．斜坡AB的长为200$\sqrt{13}$米，斜坡BC的长为200$\sqrt{2}$米，坡度是1：1，已知A点海拔121米，C点海拔721米．
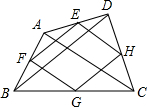如图，连接四边形ABCD各边中点，得到四边形EFGH，只要添加AC=BD条件，就能保证四边形EFGH是菱形．