题目内容
16. 如图,AB∥CD,下列结论中错误的是( )
如图,AB∥CD,下列结论中错误的是( )| A. | ∠1=∠2 | B. | ∠2+∠5=180° | C. | ∠2+∠3=180° | D. | ∠3+∠4=180° |
分析 直接根据平行线的性质对A、D进行判断;利用等量代换可对B进行判断;由于没有已知EF∥GH,∠2+∠3=180°不能确定,于是可对C进行判断.
解答 解:∵AB∥CD,
∴∠1=∠2,∠3+∠4=180°,所以A、D选项说法正确
∵∠1+∠5=180°,
∴∠2+∠5=180°,所以B选项的结论正确,
∠2+∠3=180°不能确定,所以C选项的结论错误.
故选C.
点评 本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.

练习册系列答案
相关题目
4.已知:顺次连接矩形各边的中点,得到一个菱形,如图①;再顺次连接菱形各边的中点,得到一个新的矩形,如图②;然后顺次连接新的矩形各边的中点,得到一个新的菱形,如图③;如此反复操作下去,则第2014个图形中直角三角形的个数有( )
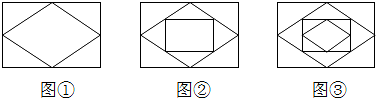

| A. | 2014个 | B. | 2015个 | C. | 4028个 | D. | 6042个 |
8.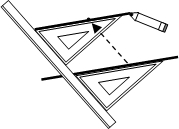 如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
 如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )| A. | 两直线平行,同位角相等 | B. | 内错角相等,两直线平行 | ||
| C. | 同旁内角互补,两直线平行 | D. | 同位角相等,两直线平行 |
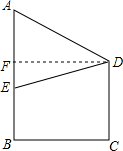 如图,某地为响应市政府“形象重于生命”的号召,在甲建筑物上从点A到点E挂一长为30米的宣传条幅,在乙建筑物的顶部D点测得条幅顶端A点的仰角为40°,测得条幅底端E的俯角为26°,求甲、乙两建筑物的水平距离BC的长(精确到0.1米).
如图,某地为响应市政府“形象重于生命”的号召,在甲建筑物上从点A到点E挂一长为30米的宣传条幅,在乙建筑物的顶部D点测得条幅顶端A点的仰角为40°,测得条幅底端E的俯角为26°,求甲、乙两建筑物的水平距离BC的长(精确到0.1米). 如图,已知△ABC的内切圆⊙O,若∠DEF=54°,则∠BAC等于72°.
如图,已知△ABC的内切圆⊙O,若∠DEF=54°,则∠BAC等于72°. 如图,在△ABC中,P为AB上一点,则下列四个条件中
如图,在△ABC中,P为AB上一点,则下列四个条件中 如图,点D、E、F分别在△ABC的三边上,DE∥AC,DF∥AB,已知∠1=55°,则∠2=55°.
如图,点D、E、F分别在△ABC的三边上,DE∥AC,DF∥AB,已知∠1=55°,则∠2=55°.