题目内容
6.(1)阅读理解已知:如图1,△ABC中,AD是中线,点P在AD上,BP、CP的延长线分别交AC、AB于E、F.求证:EF∥BC.
证明:如图2,EF交AD于G,过P作MN∥BC分别交AB、AC于M、N,
在△ABD中,由PM∥BD,得到$\frac{PM}{BD}$=$\frac{AP}{AD}$,同理$\frac{PN}{DC}$=$\frac{AP}{AD}$,
因为BD=CD,所以PM=PN.
在△FBC中,由PM∥BC,所以$\frac{PM}{BC}$=$\frac{PF}{CF}$,同理$\frac{PE}{EB}$=$\frac{PN}{BC}$∴$\frac{PF}{FC}$=$\frac{PE}{BE}$∴$\frac{PE}{PB}$=$\frac{PF}{PC}$,
∵∠EPF∠BPC,所以△EPF∽△CPB,所以∠FEP=∠PBC,所以EF∥BC.
(2)逆向思考
在△ABC中,D在BC上,点P在AD上,BP、CP的延长线分别交AC、AB于E、F,如果EF∥BC.那么D是BC中点.请你给出证明.
(3)知识应用
①如图3直线a、b、c、d、e、f、g、h是等距的一组平行线,AB在直线g上,请你用无刻度的直尺利用现有平行线作出线段AB的中点.并作简要的画图说明.
②如图4直线a、b、c、d、e、f、g、h是等距的一组平行线,点P不在这些直线上,点A在直线g上,点B在直线c上,请你用无刻度的直尺利用现有平行线作出过点P的直线PQ平行于AB.并作简要的画图说明.

分析 (2)根据相似三角形的性质可得$\frac{FG}{BD}$=$\frac{AF}{AB}$,$\frac{AF}{AB}$=$\frac{FE}{BC}$,$\frac{FE}{BC}$=$\frac{PF}{PC}$,$\frac{PF}{PC}$=$\frac{FG}{DC}$,由此即可得到BD=CD;
(3)①结合(2)中的结论,可在直线c上取一点C,连接AC交直线e于点E,连接BC交直线e于点D,连接AD、BE,交于点F,连接CF并延长,交直线g于点G,如图3,点G即为AB的中点;②结合(1)中的结论,可连接BP并延长,交直线g于点C,设AB与直线e的交点为D,连接CD、AP,交于点E,连接BE并延长,交直线g于点Q,过点P、Q作直线PQ,如图4,直线PQ即为所求作.
解答 (2)证明:设EF交AD于G,如图1.
∵FG∥BD,
∴△AFG∽和△ABD,
∴$\frac{FG}{BD}$=$\frac{AF}{AB}$.
同理:$\frac{AF}{AB}$=$\frac{FE}{BC}$,$\frac{FE}{BC}$=$\frac{PF}{PC}$,$\frac{PF}{PC}$=$\frac{FG}{DC}$,
∴$\frac{FG}{BD}$=$\frac{AF}{AB}$=$\frac{FE}{BC}$=$\frac{PF}{PC}$=$\frac{FG}{DC}$,
∴BD=CD;
(3)解:①在直线c上取一点C,连接AC交直线e于点E,连接BC交直线e于点D,连接AD、BE,交于点F,
连接CF并延长,交直线g于点G,如图3,点G即为AB的中点;
②连接BP并延长,交直线g于点C,设AB与直线e的交点为D,连接CD、AP,交于点E,
连接BE并延长,交直线g于点Q,过点P、Q作直线PQ,如图4,直线PQ即为所求作.
点评 本题是一道阅读理解题,主要考查了相似三角形的判定与性质的运用,考查了动手能力以及运用已有知识解决问题的能力,是一道好题.

 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案 如图,在矩形ABCD中,AD=2AB,点M、N分别在边AD、BC上,连接BM、DN.若四边形MBND是菱形,则$\frac{AM}{MD}$等于( )
如图,在矩形ABCD中,AD=2AB,点M、N分别在边AD、BC上,连接BM、DN.若四边形MBND是菱形,则$\frac{AM}{MD}$等于( )| A. | $\frac{3}{8}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
(1)全等三角形是相似三角形
(2)顶角相等的两个等腰三角形是相似三角形
(3)所有的等边三角形都相似
(4)有一组对边平行,另一组对边相等的四边形一定是等腰梯形.
其中真命题的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
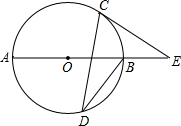 如图,AB是⊙O的直径,C,D 是⊙O上的点,∠CDB=30°,过点C作⊙O的切线交AB的延长线于E,则sinE的值为( )
如图,AB是⊙O的直径,C,D 是⊙O上的点,∠CDB=30°,过点C作⊙O的切线交AB的延长线于E,则sinE的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
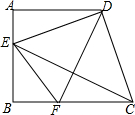 如图,已知在梯形ABCD中,AD∥BC,∠A=90°,AB=AD,点E在边AB上,且DE⊥CD,DF平分∠EDC,交BC于点F,联结CE、EF.
如图,已知在梯形ABCD中,AD∥BC,∠A=90°,AB=AD,点E在边AB上,且DE⊥CD,DF平分∠EDC,交BC于点F,联结CE、EF. 如图,已知△ABC的内切圆⊙O,若∠DEF=54°,则∠BAC等于72°.
如图,已知△ABC的内切圆⊙O,若∠DEF=54°,则∠BAC等于72°. 如图,∠1=121°,∠2=120°,∠3=120°,试写出其中的平行线,并说明理由.
如图,∠1=121°,∠2=120°,∠3=120°,试写出其中的平行线,并说明理由.