题目内容
2．在△ABC中，AB=5，AC=3，AE是△ABC的角平分线，则△ABE与△ACE的面积之比是5：3．分析 根据角平分线的性质，可得出△ABE的边AB上的高与△ACE的AC上的高相等，根据三角形的面积公式，即可得出△ABE与△ACE的面积之比等于对应边之比．
解答 解：∵AE是△ABC的角平分线，
∴设△ABE的边AB上的高与△ACE的AC上的高分别为h1，h2，
∴h1=h2，
∴△ABE与△ACE的面积之比=AB：AC=5：3，
故答案为5：3．
点评 本题考查了角平分线的性质，以及三角形的面积公式，熟练掌握三角形角平分线的性质是解题的关键．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
12．已知点C在线段AB所在的直线上，AB=8，BC=4，M是AC的中点，则MA等于（ ）
| A． | 2 | B． | 6 | C． | 2或6 | D． | 12 |
在平行四边形ABCD中，过点A作两邻边CB，CD的垂线段AP，AQ，连接PQ，作AM⊥PQ于点M，作PN⊥AQ于点N，AM，PN交于点K，AC中点为点O，当点K，O，Q在同一条直线上时，若PQ=3.5，AC=4，则AK的长度为$\frac{\sqrt{15}}{2}$．
17．关于x的一元二次方程（m+3）x2+x+m2-9=0有一个根为0，则m的值应为（ ）
| A． | 3 | B． | -3 | C． | 3或-3 | D． | 9 |
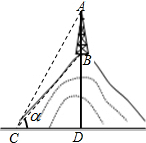如图，在铅直高度为200m的小山上建有一座电视转播塔，某数学兴趣小组为测量电视转播塔的高度，在山脚的C处测得山顶B的仰角为30°（即∠BCD=30°），测得塔顶的仰角为45°（即∠ACD=45°），请根据以上数据求塔高AB．（精确到1m．备用数据：$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732）．
已知如图，射线OC的端点O在直线AB上，∠AOC的度数比∠BOC度数的2倍多6°，则∠AOC的度数为122°．