Question

14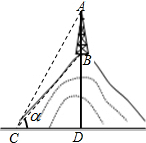．如图，在铅直高度为200m的小山上建有一座电视转播塔，某数学兴趣小组为测量电视转播塔的高度，在山脚的C处测得山顶B的仰角为30°（即∠BCD=30°），测得塔顶的仰角为45°（即∠ACD=45°），请根据以上数据求塔高AB．（精确到1m．备用数据：$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732）．

Answer 1

分析 设塔高AB为xm，根据正切的定义列出关于x的关系式，求出x即可．

解答 解：设塔高AB为xm，则AD=（200+x）m，
∵∠ACD=45°，
∴CD=AD=（200+x）m，
tan∠BCD=$\frac{BD}{CD}$，∠BCD=30°，
则$\frac{200}{200+x}$=$\frac{\sqrt{3}}{3}$，
解得x=200$\sqrt{3}$-200≈100．
答：塔高AB约为100m．

点评 本题考查的是解直角三角形的应用-仰角俯角问题，熟记锐角三角函数的概念、正确理解仰角和俯角的概念是解题的关键．