题目内容
3. 综合与实践:折纸中的数学
综合与实践:折纸中的数学数学活动课上,老师组织各学习小组同学动手操作,大胆猜想并加以验证.
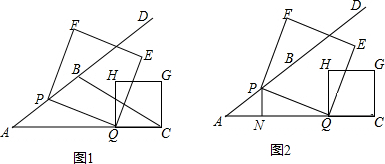
动手操作:如图,将长与宽的比是2:1的矩形纸片ABCD对折,使得点B与点A重合,点C与点D重合,然后展开,得到折痕EF,BC边上存在一点G,将角B沿GH折叠,点B落到AD边上的点B′处,点B在AB边上;将角C沿GD折叠,点C恰好落到B′G上的点C′处,HG和DG分别交EF于点M和点N,B′G交EF于点O,连接B′M,B′N.
提出猜想:①“希望”小组猜想:HG⊥DG;
②“奋斗”小组猜想:B′N⊥DG;
③“创新”小组猜想:四边形B′MGN是矩形.
独立思考:
(1)请你验证上述学习小组猜想的三个结论;(写出解答过程)
(2)假如你是该课堂的一名成员,请你在现有图形中,找出一个和四边形B′MGN面积相等的四边形.(直接写出其名称,不必证明)
分析 (1)①由∠BGH=∠B′GH,∠DGC=∠DGB′即可证明;
②只要证明△B′DG是等腰三角形即可;
③只要证明OM=OB′=OG即可;
(2)根据等腰三角形的性质、矩形的性质即可得到答案.
解答 (1)解:∵∠BGH=∠B′GH,∠DGC=∠DGB′,
∴2∠B′GH+2∠DGB′=180°,
∴∠B′GH+∠DGB′=90°,
∴∠DGH=90°即HG⊥DG,故①正确,
∵AD∥BC,
∴∠B′DG=∠DGC=∠DGB′,
∴B′D=B′G
∵AD∥EF∥BC,
AE=EB,DF=FC,
∴DN=NG,B′O=OG,
∴B′N⊥DG,故②正确,
∵OM∥BG,
∴∠OMG=∠MGB=∠MGO,
∴MO=OG=OB′,
∴△B′MG是直角三角形,
∴∠B′MG=90°,
∵∠B′MG=∠B′NG=∠NGM=90°,
∴四边形B′MGN是矩形,故③正确;
(2)结论:四边形B′MND和四边形B′MGN的面积相等.
理由:∵△B′DG是等腰三角形,DN=NG,
∴S△B′ND=S△B′NG,
∵S△B′MG=S△B′MN,
∴S四边形B′MGN=S四边形B′MND.
点评 本题考查的是翻折变换、等腰三角形的判定和性质、直角三角形的判定定理,掌握翻折变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.已知点D与点A(-2,0),B(0,4),C(a,a)是一平行四边形的四个顶点,则CD长的最小值为( )
| A. | 4 | B. | 2$\sqrt{5}$ | C. | 3$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
8.下表是截至到2002年菲尔兹奖得主获奖时的年龄:
根据表格中的信息计算获菲尔兹奖得主获奖时的平均年龄.
| 年龄 | 28≤X<30 | 30≤X<32 | 32≤X<34 | 34≤X<36 | 36≤X<38 | 38≤X<40 | 40≤X<42 |
| 频数 | 4 | 3 | 8 | 7 | 9 | 11 | 2 |
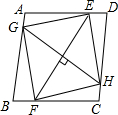 如图,在平行四边形ABCD中,E,G,F,H分别是边AD,AB,BC,CD上的点,且EF=GH,AE=CF,DH=BG,求证:四边形EGFH是菱形.
如图,在平行四边形ABCD中,E,G,F,H分别是边AD,AB,BC,CD上的点,且EF=GH,AE=CF,DH=BG,求证:四边形EGFH是菱形. 如图,在四边形ABCD中,AD∥BC,且AD<BC,AD=6cm,BC=10cm,动点P、Q分别从A、C同时出发,点P以1cm/秒的速度由A向D运动,点Q以2cm/秒的速度由C向B运动,其中一动点达到端点时,另一动点随之停止运动.
如图,在四边形ABCD中,AD∥BC,且AD<BC,AD=6cm,BC=10cm,动点P、Q分别从A、C同时出发,点P以1cm/秒的速度由A向D运动,点Q以2cm/秒的速度由C向B运动,其中一动点达到端点时,另一动点随之停止运动.