题目内容
18.已知点D与点A(-2,0),B(0,4),C(a,a)是一平行四边形的四个顶点,则CD长的最小值为( )| A. | 4 | B. | 2$\sqrt{5}$ | C. | 3$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
分析 讨论两种情形:①CD是对角线,②CD是边.CD是对角线时CF⊥直线y=x时,CD最小.CD是边时,CD=AB=2$\sqrt{5}$,通过比较即可得出结论.
解答 解:如图如果AB、CD为对角线,AB与CD交于点F,当FC⊥直线y=x时,CD最小.
设直线AB为y=kx+b则$\left\{\begin{array}{l}{b=4}\\{-2k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=2}\\{b=4}\end{array}\right.$.
∴直线AB为y=2x+4,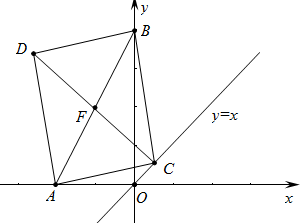
∵AF=FB,
∴点F坐标为(-1,2),
∵CF⊥直线y=x,
设直线CF为y=-x+b′F(-1,2)代入得b′=1
∴直线CF为y=-x+1,
由$\left\{\begin{array}{l}{y=x}\\{y=-x+1}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\frac{1}{2}}\\{y=\frac{1}{2}}\end{array}\right.$,
∴点C坐标($\frac{1}{2}$,$\frac{1}{2}$).
∴CD=2CF=2×$\sqrt{(\frac{1}{2}+1)^{2}+(\frac{1}{2}-2)^{2}}$=3$\sqrt{2}$.
如果CD是平行四边形的边,则CD=AB=2$\sqrt{5}$>3$\sqrt{2}$,
∴CD的最小值为3$\sqrt{2}$.
故选C.
点评 本题考查平行四边形的性质、坐标与图形的性质、垂线段最短等知识,学会分类讨论是解题的关键,灵活运用垂线段最短解决实际问题,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
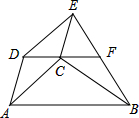 如图,四边形ABCD中,AB∥DC,以AC,AD为边作?ACED,DG的延长线交BE于F,求证:EF=FB.(请用多种证明方法)
如图,四边形ABCD中,AB∥DC,以AC,AD为边作?ACED,DG的延长线交BE于F,求证:EF=FB.(请用多种证明方法)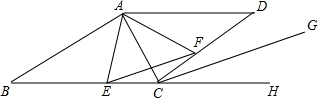
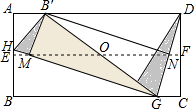 综合与实践:折纸中的数学
综合与实践:折纸中的数学