题目内容
13.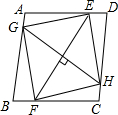 如图,在平行四边形ABCD中,E,G,F,H分别是边AD,AB,BC,CD上的点,且EF=GH,AE=CF,DH=BG,求证:四边形EGFH是菱形.
如图,在平行四边形ABCD中,E,G,F,H分别是边AD,AB,BC,CD上的点,且EF=GH,AE=CF,DH=BG,求证:四边形EGFH是菱形.
分析 由平行四边形的性质和已知条件得出∠A=∠C,AG=CH,由SAS证明△AGE≌△FHC,得出GE=FH,同理:GF=EH,证出四边形EGFH是平行四边形,再由对角线互相垂直,即可得出结论.
解答 证明:∵四边形ABCD是平行四边形,
∴AB=CD,∠A=∠C,
∵DH=BG,
∴AG=CH,
在△AGE和△FHC中,$\left\{\begin{array}{l}{AE=CF}&{\;}\\{∠A=∠C}&{\;}\\{AG=CH}&{\;}\end{array}\right.$,
∴△AGE≌△FHC)SAS),
∴GE=FH,
同理:GF=EH,∴四边形EGFH是平行四边形,
又∵EF⊥GH,
∴四边形EGFH是菱形.
点评 本题考查了菱形的判定、全等三角形的判定与性质、平行四边形的判定与性质;熟练掌握平行四边形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案
相关题目
1.下列语句中,不是命题的是( )
| A. | 两点之间线段最短 | B. | 连接A、B两点 | ||
| C. | 平行于同一直线的两直线平行 | D. | 相等的角都是直角 |
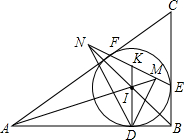 如图,△ABC的内切圆I在边AB,BC,CA上的切点分别是D,E,F,直线EF与直线AI,BI,DI分别相交于点M,N,K.
如图,△ABC的内切圆I在边AB,BC,CA上的切点分别是D,E,F,直线EF与直线AI,BI,DI分别相交于点M,N,K.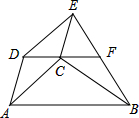 如图,四边形ABCD中,AB∥DC,以AC,AD为边作?ACED,DG的延长线交BE于F,求证:EF=FB.(请用多种证明方法)
如图,四边形ABCD中,AB∥DC,以AC,AD为边作?ACED,DG的延长线交BE于F,求证:EF=FB.(请用多种证明方法)
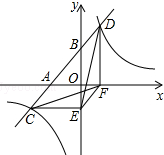 如图,一次函数y=ax+b与x轴、y轴交于A、B两点,与反比例函数y=$\frac{k}{x}$相交于C、D两点,分别过C、D两点作y轴、x轴的垂线,垂足为E、F,连接CF、DE、EF. 有下列三个结论:①△CEF与△DEF的面积相等;②△DCE≌△CDF;③AC=BD.其中正确的结论个数是( )
如图,一次函数y=ax+b与x轴、y轴交于A、B两点,与反比例函数y=$\frac{k}{x}$相交于C、D两点,分别过C、D两点作y轴、x轴的垂线,垂足为E、F,连接CF、DE、EF. 有下列三个结论:①△CEF与△DEF的面积相等;②△DCE≌△CDF;③AC=BD.其中正确的结论个数是( ) 如图,在?ABCD中,AB=AC,若?ABCD的周长为38,△ABC的周长比?ABCD的周长少10,求AB和BC的长.
如图,在?ABCD中,AB=AC,若?ABCD的周长为38,△ABC的周长比?ABCD的周长少10,求AB和BC的长.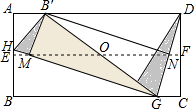 综合与实践:折纸中的数学
综合与实践:折纸中的数学