题目内容
11.如图:在△ABC中,AB=5,AC=9,S△ABC=$\frac{27}{2}$,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,动点Q从C点出发,以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH.(1)tanA=$\frac{3}{4}$;
(2)过P作PN⊥AC于N,设点P运动时间为t,
①PN=3t,QN=9-9t(用含t的代数式表示);
②若正方形PQEF的面积为S,请探究S是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由;
(3)当t为何值时,正方形PQEF的某个顶点(Q除外)落在正方形QCGH的边上,请直接写出t的值.
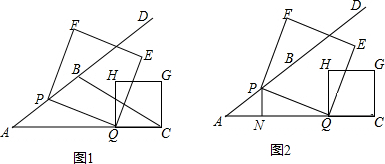
分析 (1)如图1,过点B作BM⊥AC于点M,利用面积法求得BM的长度,利用勾股定理得到AM的长度,最后由锐角三角函数的定义进行解答;
(2)如图2,①过点P作PN⊥AC于点N,根据题意即可得到结果;②利用(1)中的结论和勾股定理得到PN2+NQ2=PQ2,所以由正方形的面积公式得到S关于t的二次函数,利用二次函数的顶点坐标公式和二次函数图象的性质来求其最值;
(3)需要分类讨论:当点E在边HG上、点F在边HG上、点P边QH(或点E在QC上)、点F边C上时相对应的t的值.
解答 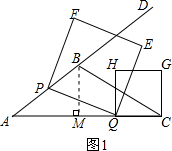 解:(1)如图1,过点B作BM⊥AC于点M,
解:(1)如图1,过点B作BM⊥AC于点M,
∵AC=9,S△ABC=$\frac{27}{2}$,
∴$\frac{1}{2}$AC•BM=$\frac{27}{2}$,即$\frac{1}{2}$×9•BM=$\frac{27}{2}$,
解得BM=3.
由勾股定理,得
AM=$\sqrt{A{B}^{2}-B{M}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
则tanA=$\frac{BM}{AM}$=$\frac{3}{4}$;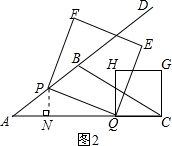
故答案为:$\frac{3}{4}$;
(2)存在,
①如图2,过点P作PN⊥AC于点N,
依题意得AP=CQ=5t,
∵tanA=$\frac{3}{4}$,
∴AN=4t,PN=3t,
∴QN=AC-AN-CQ=9-9t,
故答案为:3t,9-9t;
②根据勾股定理得到:PN2+NQ2=PQ2,
S正方形PQEF=PQ2=(3t)2+(9-9t)2=90t2-162t+81(0<t<$\frac{9}{5}$).
∵-$\frac{b}{2a}$=$\frac{-162}{2×90}$=$\frac{9}{10}$,在t的取值范围之内,
∴S最小值=$\frac{4ac-{b}^{2}}{4a}$=$\frac{4×90×81-16{2}^{2}}{4×90}$=$\frac{81}{10}$;
(3)①如图3,当点E在边HG上时,过P作PN⊥AC于N,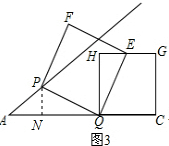
由②知,NQ=9-9t,
∵四边形PQEF,QCGH是正方形,
∴PQ=QE,∠CQH=∠PQE=90°,
∴∠PQN=∠EQH,
在△PQN与△HQE中,$\left\{\begin{array}{l}{∠PNQ=∠H=90°}\\{∠PQN=∠HQE}\\{PQ=QE}\end{array}\right.$,
∴△PQN≌△HQE,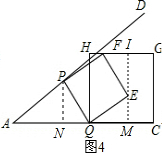
∴QN=HQ,
∴9-9t=5t,
解得t1=$\frac{9}{14}$;
②如图4,当点F在边HG上时,过E作ME⊥CQ于M,反向延长EM交HG于I,
则四边形HQMI是矩形,
∴IM=HQ=5t,
在△PNQ与△QEM中,$\left\{\begin{array}{l}{∠QPN=∠EQM}\\{∠PNQ=∠QME}\\{PQ=EQ}\end{array}\right.$,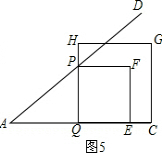
∴△PNQ≌△QEN,
∴PN=QM=3t,ME=NQ=9-9t,
同理△FIE≌△QEN,
∴IE=QM-3t,
∴ME=2t,
∴2t=9-9t,
解得:t2=$\frac{9}{11}$;
③如图5,当点P边QH(或点E在QC上)时,∵PQ⊥CQ,
∴AQ=4t,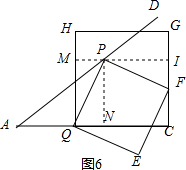
∴9t=9,解得:t3=1;
④如图6,当点F边CG上时,过P作PN⊥AC于N,PM⊥HQ于M,反向延长交QC于I,
则四边形PMQN是矩形,
∴PM=QN=9t-9,
同理证得△PNQ≌△PIF,
∴PI=PN=3t,
∴PM=2t
∴2t=9t-9,
解得:t4=$\frac{9}{7}$.
点评 本题考查了四边形综合题.其中涉及到了三角形的面积公式,正方形的性质,勾股定理以及二次函数的最值的求法.其中,解答(3)题时,要分类讨论,做到不重不漏,结合图形解题,更形象、直观.

 如图,在?ABCD中,AB=AC,若?ABCD的周长为38,△ABC的周长比?ABCD的周长少10,求AB和BC的长.
如图,在?ABCD中,AB=AC,若?ABCD的周长为38,△ABC的周长比?ABCD的周长少10,求AB和BC的长. 如图,在?ABCD中,AE是∠BAD的平分线交DC于点E,求证:CE+BC=AB.
如图,在?ABCD中,AE是∠BAD的平分线交DC于点E,求证:CE+BC=AB.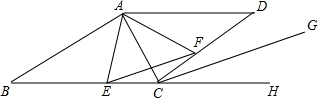

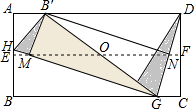 综合与实践:折纸中的数学
综合与实践:折纸中的数学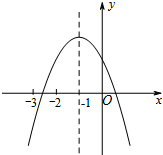 如图是二次函数y=ax2+bx+c图象的一部分,过点(x1,0),-3<x1<-2,对称轴为直线x=-1.给出四个结论:①abc>0;②2a+b=0;③b2>4ac;④3b+2c>0,其中正确的结论有( )
如图是二次函数y=ax2+bx+c图象的一部分,过点(x1,0),-3<x1<-2,对称轴为直线x=-1.给出四个结论:①abc>0;②2a+b=0;③b2>4ac;④3b+2c>0,其中正确的结论有( )