题目内容
 如图,在四边形ABCD中,对角线AC,BD相交于点O,AB∥CD,AO=OC.
如图,在四边形ABCD中,对角线AC,BD相交于点O,AB∥CD,AO=OC.求证:(1)△AOB≌△COD;
(2)四边形ABCD是平行四边形.
考点:平行四边形的判定,全等三角形的判定与性质
专题:证明题
分析:(1)首先根据平行线的性质可得∠1=∠2,∠3=∠4.然后再利用AAS定理证明△AOB≌△COD;
(2)根据△AOB≌△COD可得BO=DO,再根据对角线互相平分的四边形是平行四边形可得四边形ABCD是平行四边形.
(2)根据△AOB≌△COD可得BO=DO,再根据对角线互相平分的四边形是平行四边形可得四边形ABCD是平行四边形.
解答: 证明:(1)∵AB∥CD,
证明:(1)∵AB∥CD,
∴∠1=∠2,∠3=∠4.
在△AOB和△COD中,
,
∴△AOB≌△COD(AAS);
(2)∵△AOB≌△COD,
∴BO=DO,
又∵AO=OC,
∴四边形ABCD是平行四边形.
 证明:(1)∵AB∥CD,
证明:(1)∵AB∥CD,∴∠1=∠2,∠3=∠4.
在△AOB和△COD中,
|
∴△AOB≌△COD(AAS);
(2)∵△AOB≌△COD,
∴BO=DO,
又∵AO=OC,
∴四边形ABCD是平行四边形.
点评:此题主要考查了全等三角形的判定,以及平行四边形的判定,关键是掌握对角线互相平分的四边形是平行四边形.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
顶点为(-5,-1),且开口方向,形状与函数y=-
x2的图象相同的抛物线是( )
| 1 |
| 3 |
A、y=
| ||
B、y=-
| ||
C、y=-
| ||
D、y=
|
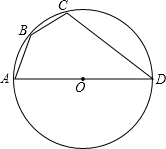 已知:四边形ABCD内接于以AD为直径的⊙O,且AD=4,AB=CB=1,求:CD的长.
已知:四边形ABCD内接于以AD为直径的⊙O,且AD=4,AB=CB=1,求:CD的长.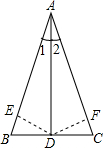 已知在△ABC中,D是BC的中点,∠1=∠2,求证:AB=AC.
已知在△ABC中,D是BC的中点,∠1=∠2,求证:AB=AC.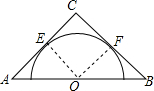 如图所示,在△ABC中,有一半圆内切AC、BC分别于E、F,半圆圆心在AB上,且已知AC=b,BC=a,∠ACB=θ,求半圆的半径.
如图所示,在△ABC中,有一半圆内切AC、BC分别于E、F,半圆圆心在AB上,且已知AC=b,BC=a,∠ACB=θ,求半圆的半径.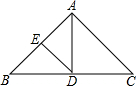 在等腰△ABC中,AB=AC=8,∠B=40°,AD是∠BAC的平分线,交BC于D,点E是AB的中点,连接DE.求:
在等腰△ABC中,AB=AC=8,∠B=40°,AD是∠BAC的平分线,交BC于D,点E是AB的中点,连接DE.求: