题目内容
8.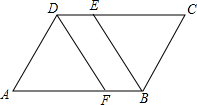 如图,在四边形ABCD中,AB∥CD,AD∥BC,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F
如图,在四边形ABCD中,AB∥CD,AD∥BC,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F(1)若∠A=75°,则∠CEB的度数为52.5°;
(2)是判断DF与BE是否平行,并说明理由.
分析 (1)由平行线的性质可求得∠ABC=105°,由角平分线的定义可求得∠ABE,再根据平行线的性质可求得∠ABE=∠CEB,可求得答案;
(2)由条件可先证明∠ABC=∠ADC,结合角平分线的定义可证明∠CEB=∠CDF,可证得DF∥BE.
解答 解:
(1)∵AD∥BC,
∴∠ABC=180°-∠A=180°-75°=105°,
∵BE平分∠ABC,
∴∠ABE=$\frac{1}{2}$∠ABC=52.5°,
∵AB∥CD,
∴∠CEB=∠ABE=52.5°,
故答案为:52.5°;
(2)平行.理由如下:
∵AB∥CD,
∴∠ADC+∠A=180°,∠ABE=∠CEB,
∵AD∥BC,
∴∠A+∠ABC=180°,
∴∠ABC=∠ADC,
∵∠CDF=$\frac{1}{2}$∠ADC,∠ABE=$\frac{1}{2}$∠ABC,
∴∠CDF=∠ABE,
∴∠CDF=∠CEB,
∴DF∥BE.
点评 本题主要考查平行线的判定和性质,掌握平行线的判定和性质是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c⇒a∥c.

练习册系列答案
相关题目
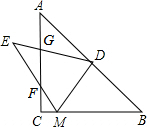 如图,点D是等腰直角△ABC斜边AB的中点,M是边BC上的点,将△DBM沿DM折叠,点B的对称点E落在直线AC的左侧,EM交边AC于点F,ED交边AC于点G.
如图,点D是等腰直角△ABC斜边AB的中点,M是边BC上的点,将△DBM沿DM折叠,点B的对称点E落在直线AC的左侧,EM交边AC于点F,ED交边AC于点G. 如图,在一单位长度为1cm的方格纸上,依如图所示的规律,设定点A1、A2、A3、A4、A5、A6、A7、…、An,连接点O、A1、A2组成三角形,记为△1,连接O、A2、A3组成三角形,记为△2…,连O、An、An+1组成三角形,记为△n(n为正整数),请你推断,当n为50时,△n的面积=( )cm2.
如图,在一单位长度为1cm的方格纸上,依如图所示的规律,设定点A1、A2、A3、A4、A5、A6、A7、…、An,连接点O、A1、A2组成三角形,记为△1,连接O、A2、A3组成三角形,记为△2…,连O、An、An+1组成三角形,记为△n(n为正整数),请你推断,当n为50时,△n的面积=( )cm2.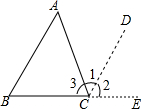 阅读并填空:
阅读并填空: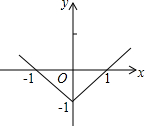 一次函数y=x-1的图象是一条直线,函数y=|x|-1的图象具有怎样的形状呢?
一次函数y=x-1的图象是一条直线,函数y=|x|-1的图象具有怎样的形状呢? 如图,点E、F在BD上,且AB=CD,BF=DE,AE=CF,AC与BD相交于点O,求证:AE∥CF.
如图,点E、F在BD上,且AB=CD,BF=DE,AE=CF,AC与BD相交于点O,求证:AE∥CF.