题目内容
16. 阅读并填空:
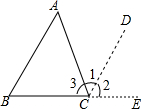
阅读并填空:已知:如图,在△ABC中,试说明∠A+∠B+∠C=180°的理由.
理由:过点C作∠ACD=∠A,并延长BC到E.
∵∠1=∠A;(已作),
∴AB∥CD内错角相等,两直线平行,
∴∠B=∠2(两直线平行,同位角相等),
∵∠1+∠2+∠3=180°,(平角的定义),
∴∠A+∠B+∠ACB=180°(等量代换)
分析 由条件可证明AB∥CD,可得∠B=∠2,结合平角的定义可证明∠A+∠B+∠ACB=180°.
解答 解:∵∠1=∠A;(已作),
∴AB∥CD 内错角相等,两直线平行,
∴∠B=∠2(两直线平行,同位角相等),
∵∠1+∠2+∠3=180°,(平角的定义),
∴∠A+∠B+∠ACB=180°(等量代换).
故答案为:内错角相等,两直线平行;∠2;平角的定义.
点评 本题主要考查平行线的判定和性质,掌握平行线的判定和性质是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c⇒a∥c.

练习册系列答案
相关题目
7. 二次函数y=ax2+b的图象如图所示,则下列判断正确的是( )
二次函数y=ax2+b的图象如图所示,则下列判断正确的是( )
 二次函数y=ax2+b的图象如图所示,则下列判断正确的是( )
二次函数y=ax2+b的图象如图所示,则下列判断正确的是( )| A. | a>0,b<0 | B. | a>0,b>0 | C. | a<0,b<0 | D. | a<0,b>0 |
4.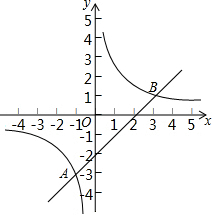 已知一次函数y1=kx+b(k>0)与反比例函数y2=$\frac{m}{x}$(m≠0)的图象相交于A(-1,a),B(3,b)两点,当y1>y2时,实数x的取值范围是( )
已知一次函数y1=kx+b(k>0)与反比例函数y2=$\frac{m}{x}$(m≠0)的图象相交于A(-1,a),B(3,b)两点,当y1>y2时,实数x的取值范围是( )
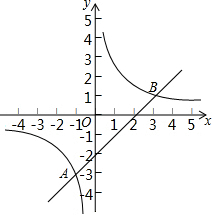 已知一次函数y1=kx+b(k>0)与反比例函数y2=$\frac{m}{x}$(m≠0)的图象相交于A(-1,a),B(3,b)两点,当y1>y2时,实数x的取值范围是( )
已知一次函数y1=kx+b(k>0)与反比例函数y2=$\frac{m}{x}$(m≠0)的图象相交于A(-1,a),B(3,b)两点,当y1>y2时,实数x的取值范围是( )| A. | x<-1或0<x<3 | B. | -1<x<0或0<x<3 | C. | -1<x<0或x>3 | D. | 0<x<3 |
 如图,一只蚂蚁以均匀的速度沿台阶A1→A2→A3→A4→A5爬行,则此蚂蚁爬行的高度h随时间t变化的图象大致是( )
如图,一只蚂蚁以均匀的速度沿台阶A1→A2→A3→A4→A5爬行,则此蚂蚁爬行的高度h随时间t变化的图象大致是( )



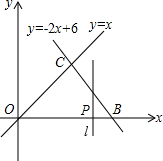 如图,直线OC,BC的解析式分别为y=x和y=-2x+6,动点P(t,0)在线段OB上移动(不与O,B重合),过点P作直线l与x垂直.
如图,直线OC,BC的解析式分别为y=x和y=-2x+6,动点P(t,0)在线段OB上移动(不与O,B重合),过点P作直线l与x垂直.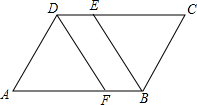 如图,在四边形ABCD中,AB∥CD,AD∥BC,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F
如图,在四边形ABCD中,AB∥CD,AD∥BC,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F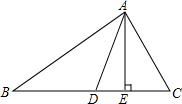 如图,已知AD、AE分别为△ABC的中线、高,且AB=5cm,AC=3cm,求:
如图,已知AD、AE分别为△ABC的中线、高,且AB=5cm,AC=3cm,求: