题目内容
18.观察并解答下列问题:(1)填空:①(x-1)(x+1)=x2-1
②(x-1)(x2+x+1)=x3-1
③(x-1)(x3+x2+x+1)=x4-1
④(x-1)(x4+x3+x2+x+1)=x5-1
(2)你有什么猜想,能否据此给出一个带有一般性的结论?
分析 (1)利用多项式乘多项式法则进行计算;
(2)通过计算找出其中的规律,然后用含字母n的式子表示规律.
解答 解:(1)(x-1)(x+1)=x2-1;
(x-1)(x2+x+1)=x3-1;
(x-1)(x3+x2+x+1)=x4-1;
(x-1)(x4+x3+x2+x+1)=x5-1
(2)(x-1)(xn+xn-1+xn-2+…x2+x+1)=xn+1-1.
点评 本题主要考查的是多项式乘多项式法则的应用,利用多项式乘多项式法则求得各式的值是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
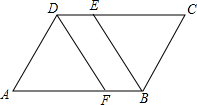 如图,在四边形ABCD中,AB∥CD,AD∥BC,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F
如图,在四边形ABCD中,AB∥CD,AD∥BC,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F 如图,在△ABC中,∠C=90°,BC=6,AC=8,AB=10,请画出AB边上的高并求出这条高的长度.
如图,在△ABC中,∠C=90°,BC=6,AC=8,AB=10,请画出AB边上的高并求出这条高的长度.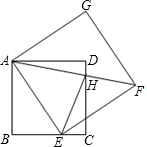 如图,E为正方形ABCD的边BC上一动点,以AE为一边作正方形AEFD,对角线AF交边CD于H,连EH.
如图,E为正方形ABCD的边BC上一动点,以AE为一边作正方形AEFD,对角线AF交边CD于H,连EH.