题目内容
20. 如图,点E、F在BD上,且AB=CD,BF=DE,AE=CF,AC与BD相交于点O,求证:AE∥CF.
如图,点E、F在BD上,且AB=CD,BF=DE,AE=CF,AC与BD相交于点O,求证:AE∥CF.
分析 利用SSS证明△ABE与△CDF全等,再利用平行线的性质证明即可.
解答 证明:∵BF=DE,
∴BF-EF=DE-EF,
即BE=DF,
在△ABE与△CDF中,
$\left\{\begin{array}{l}{AB=CD}\\{BE=DF}\\{AE=CF}\end{array}\right.$,
∴△ABE≌△CDF(SSS),
∴∠AEB=∠CFD,
∴∠AEO=∠CFO,
∴AE∥CF.
点评 此题考查全等三角形的判定和性质,关键是利用SSS证明△ABE与△CDF全等,再利用平行线的性质证明.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 如图,一只蚂蚁以均匀的速度沿台阶A1→A2→A3→A4→A5爬行,则此蚂蚁爬行的高度h随时间t变化的图象大致是( )
如图,一只蚂蚁以均匀的速度沿台阶A1→A2→A3→A4→A5爬行,则此蚂蚁爬行的高度h随时间t变化的图象大致是( )



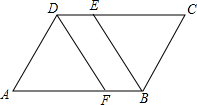 如图,在四边形ABCD中,AB∥CD,AD∥BC,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F
如图,在四边形ABCD中,AB∥CD,AD∥BC,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F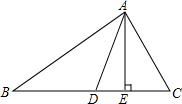 如图,已知AD、AE分别为△ABC的中线、高,且AB=5cm,AC=3cm,求:
如图,已知AD、AE分别为△ABC的中线、高,且AB=5cm,AC=3cm,求:
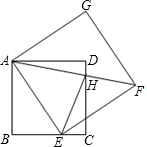 如图,E为正方形ABCD的边BC上一动点,以AE为一边作正方形AEFD,对角线AF交边CD于H,连EH.
如图,E为正方形ABCD的边BC上一动点,以AE为一边作正方形AEFD,对角线AF交边CD于H,连EH.