题目内容
5. 如图,OA在x轴上,OB在y轴上,OA=8,AB=10,点C在边OA上,AC=2,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数y=$\frac{k}{x}$(k≠0)的图象经过圆心P,则k=-5.
如图,OA在x轴上,OB在y轴上,OA=8,AB=10,点C在边OA上,AC=2,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数y=$\frac{k}{x}$(k≠0)的图象经过圆心P,则k=-5.
分析 作PD⊥OA于D,PE⊥AB于E,作CH⊥AB于H,如图,设⊙P的半径为r,根据切线的性质和切线长定理得到PD=PE=r,AD=AE,再利用勾股定理计算出OB=6,则可判断△OBC为等腰直角三角形,从而得到△PCD为等腰直角三角形,则PD=CD=r,AE=AD=2+r,通过证明△ACH∽△ABO,利用相似比计算出CH=$\frac{6}{5}$,接着利用勾股定理计算出AH=$\frac{8}{5}$,所以BH=10-$\frac{8}{5}$=$\frac{42}{5}$,然后证明△BEP∽△BHC,利用相似比得到即$\frac{10-(2+r)}{\frac{42}{5}}$=$\frac{r}{\frac{6}{5}}$,解得r=1,从而易得P点坐标,再利用反比例函数图象上点的坐标特征求出k的值.
解答 解:作PD⊥OA于D,PE⊥AB于E,作CH⊥AB于H,如图,设⊙P的半径为r,
∵⊙P与边AB,AO都相切,
∴PD=PE=r,AD=AE,
在Rt△OAB中,∵OA=8,AB=10,
∴OB=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
∵AC=2,
∴OC=6,
∴△OBC为等腰直角三角形,
∴△PCD为等腰直角三角形,
∴PD=CD=r,
∴AE=AD=2+r,
∵∠CAH=∠BAO,
∴△ACH∽△ABO,
∴$\frac{CH}{OB}$=$\frac{AC}{AB}$,即$\frac{CH}{6}$=$\frac{2}{10}$,解得CH=$\frac{6}{5}$,
∴AH=$\sqrt{A{C}^{2}-C{H}^{2}}$=$\sqrt{{2}^{2}-(\frac{6}{5})^{2}}$=$\frac{8}{5}$,
∴BH=10-$\frac{8}{5}$=$\frac{42}{5}$,
∵PE∥CH,
∴△BEP∽△BHC,
∴$\frac{BE}{BH}$=$\frac{PE}{CH}$,即$\frac{10-(2+r)}{\frac{42}{5}}$=$\frac{r}{\frac{6}{5}}$,解得r=1,
∴OD=OC-CD=6-1=5,
∴P(5,-1),
∴k=5×(-1)=-5.
故答案为-5.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线不确定切点,则过圆心作切线的垂线,则垂线段等于圆的半径.也考查了勾股定理、相似三角形的判定与性质和反比例函数图象上点的坐标特征.

| A. | (0,0) | B. | (0,2) | C. | (2,-4) | D. | (-4,2) |
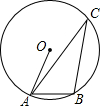 如图,A,B,C是⊙O上三点,∠ACB=25°,则∠BAO的度数是( )
如图,A,B,C是⊙O上三点,∠ACB=25°,则∠BAO的度数是( )| A. | 55° | B. | 60° | C. | 65° | D. | 70° |
 某车间接到加工一批零件的任务,准备派甲、乙两名工人参与完成.乙比甲晚参加工作一段时间,工作期间甲工人因有事停工5天,若两人分得的工作量相等,各自的工作效率一定,他们各自的工作量y(个)随工作时间x(天)变化的图象如图所示,则有下列说法:
某车间接到加工一批零件的任务,准备派甲、乙两名工人参与完成.乙比甲晚参加工作一段时间,工作期间甲工人因有事停工5天,若两人分得的工作量相等,各自的工作效率一定,他们各自的工作量y(个)随工作时间x(天)变化的图象如图所示,则有下列说法: 在矩形ABCD中,AB=5,AD=12,将矩形ABCD沿直线l向右翻滚两次至如图所示位置,则点B所经过的路线长是12.5π(结果不取近似值).
在矩形ABCD中,AB=5,AD=12,将矩形ABCD沿直线l向右翻滚两次至如图所示位置,则点B所经过的路线长是12.5π(结果不取近似值). 如图,在平行四边形ABCD中,EF∥AB交AD于E,交BD于F,DE:EA=3:4,EF=3,则CD的长为( )
如图,在平行四边形ABCD中,EF∥AB交AD于E,交BD于F,DE:EA=3:4,EF=3,则CD的长为( ) 一块直角三角板ABC按如图放置,顶点A的坐标为(0,1),直角顶点C的坐标为(-3,0),∠B=30°,则点B的坐标为(-3-$\sqrt{3}$,3$\sqrt{3}$).
一块直角三角板ABC按如图放置,顶点A的坐标为(0,1),直角顶点C的坐标为(-3,0),∠B=30°,则点B的坐标为(-3-$\sqrt{3}$,3$\sqrt{3}$).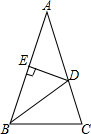 如图,在△ABC中,AB=AC,∠A=36°,BD为角平分线,DE⊥AB,垂足为E.
如图,在△ABC中,AB=AC,∠A=36°,BD为角平分线,DE⊥AB,垂足为E.