题目内容
16.在平面直角坐标系中有三个点A(1,-1)、B(-1,-1)、C(0,1),点P(0,2)关于A的对称点为P1,P1关于B的对称点P2,P2关于C的对称点为P3,按此规律继续以A、B、C为对称中心重复前面的操作,依次得到P4,P5,P6,…,则点P2015的坐标是( )| A. | (0,0) | B. | (0,2) | C. | (2,-4) | D. | (-4,2) |
分析 设P1(x,y),再根据中点的坐标特点求出x、y的值,找出规律即可得出结论.
解答 解:设P1(x,y),
∵点A(1,-1)、B(-1,-1)、C(0,1),点P(0,2)关于A的对称点为P1,P1关于B的对称点P2,
∴$\frac{x}{2}$=1,$\frac{y+2}{2}$=-1,解得x=2,y=-4,
∴P1(2,-4).
同理可得,P1(2,-4),P2(-4,2),P3(4,0),P4(-2,-2),P5(0,0),P6(0,2),P7(2,-4),…,…,
∴每6个数循环一次.
∵$\frac{2015}{6}$=335…5,
∴点P2015的坐标是(0,0).
故选A.
点评 本题考查的是点的坐标,根据题意找出规律是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.2014年4月21日8时我市各地域的可吸入颗粒物数值统计如下表:
该日这一时刻的可吸入颗粒物数值的众数和中位数分别是( )
| 地域 | 荔城 | 城厢 | 秀屿 | 涵江 | 仙游 | 湄洲 |
| 可吸入颗粒物(mg/m3) | 0.15 | 0.15 | 0.13 | 0.15 | 0.18 | 0.14 |
| A. | 0.15和0.14 | B. | 0.18和0.15 | C. | 0.18和0.14 | D. | 0.15和0.15 |
7.下列说法中正确的是( )
| A. | 在统计学中,把组成总体的每一个考察对象叫做样本容量 | |
| B. | 为了解全国中学生的心理健康情况,应该采用普查的方式 | |
| C. | 一组数据6,8,7,8,8,9,10的众数和中位数都是8 | |
| D. | 若甲组数据的方差为s12=0.4,乙组数据的方差为s12=0.05,则甲组数据更稳定 |
4. 如图,在直角∠O的内部有一滑动杆AB,当端点A沿直线AO向下滑动时,端点B会随之自动地沿直线OB向左滑动,如果滑动杆从图中AB处滑动到A′B′处,那么滑动杆的中点C所经过的路径是( )
如图,在直角∠O的内部有一滑动杆AB,当端点A沿直线AO向下滑动时,端点B会随之自动地沿直线OB向左滑动,如果滑动杆从图中AB处滑动到A′B′处,那么滑动杆的中点C所经过的路径是( )
 如图,在直角∠O的内部有一滑动杆AB,当端点A沿直线AO向下滑动时,端点B会随之自动地沿直线OB向左滑动,如果滑动杆从图中AB处滑动到A′B′处,那么滑动杆的中点C所经过的路径是( )
如图,在直角∠O的内部有一滑动杆AB,当端点A沿直线AO向下滑动时,端点B会随之自动地沿直线OB向左滑动,如果滑动杆从图中AB处滑动到A′B′处,那么滑动杆的中点C所经过的路径是( )| A. | 直线的一部分 | B. | 圆的一部分 | C. | 双曲线的一部分 | D. | 抛物线的一部分 |
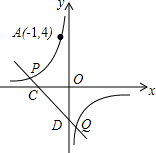 如图,反比例函数y=$\frac{k}{x}$的图象经过点A(-1,4),直线y=-x+b(b≠0)与双曲线y=$\frac{k}{x}$在第二、四象限分别相交于P,Q两点,与x轴、y轴分别相交于C,D两点.
如图,反比例函数y=$\frac{k}{x}$的图象经过点A(-1,4),直线y=-x+b(b≠0)与双曲线y=$\frac{k}{x}$在第二、四象限分别相交于P,Q两点,与x轴、y轴分别相交于C,D两点. 如图,一只蚂蚁从O点出发,沿着扇形OAB的边缘匀速爬行一周,当蚂蚁运动的时间为t时,蚂蚁与O点的距离为s,则s关于t的函数图象大致是( )
如图,一只蚂蚁从O点出发,沿着扇形OAB的边缘匀速爬行一周,当蚂蚁运动的时间为t时,蚂蚁与O点的距离为s,则s关于t的函数图象大致是( )



 如图,OA在x轴上,OB在y轴上,OA=8,AB=10,点C在边OA上,AC=2,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数y=$\frac{k}{x}$(k≠0)的图象经过圆心P,则k=-5.
如图,OA在x轴上,OB在y轴上,OA=8,AB=10,点C在边OA上,AC=2,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数y=$\frac{k}{x}$(k≠0)的图象经过圆心P,则k=-5. 如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.求证:∠CBE=∠BAD.
如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.求证:∠CBE=∠BAD.