题目内容
14.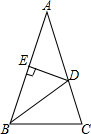 如图,在△ABC中,AB=AC,∠A=36°,BD为角平分线,DE⊥AB,垂足为E.
如图,在△ABC中,AB=AC,∠A=36°,BD为角平分线,DE⊥AB,垂足为E.(1)写出图中一对全等三角形和一对相似比不为1的相似三角形;
(2)选择(1)中一对加以证明.
分析 (1)利用相似三角形的判定以及全等三角形的判定方法得出符合题意的答案;
(2)利用相似三角形的判定以及全等三角形的判定方法分别得出即可.
解答 解:(1)△ADE≌△BDE,△ABC∽△BCD;
(2)证明:∵AB=AC,∠A=36°,
∴∠ABC=∠C=72°,
∵BD为角平分线,
∴∠ABD=$\frac{1}{2}$∠ABC=36°=∠A,
在△ADE和△BDE中
∵$\left\{\begin{array}{l}{∠A=∠DBA}\\{∠AED=∠BED}\\{ED=ED}\end{array}\right.$,
∴△ADE≌△BDE(AAS);
证明:∵AB=AC,∠A=36°,
∴∠ABC=∠C=72°,
∵BD为角平分线,
∴∠DBC=$\frac{1}{2}$∠ABC=36°=∠A,
∵∠C=∠C,
∴△ABC∽△BCD.
点评 此题主要考查了相似三角形以及全等三角形的判定,正确把握判定方法是解题关键.

练习册系列答案
相关题目
4. 如图,在直角∠O的内部有一滑动杆AB,当端点A沿直线AO向下滑动时,端点B会随之自动地沿直线OB向左滑动,如果滑动杆从图中AB处滑动到A′B′处,那么滑动杆的中点C所经过的路径是( )
如图,在直角∠O的内部有一滑动杆AB,当端点A沿直线AO向下滑动时,端点B会随之自动地沿直线OB向左滑动,如果滑动杆从图中AB处滑动到A′B′处,那么滑动杆的中点C所经过的路径是( )
 如图,在直角∠O的内部有一滑动杆AB,当端点A沿直线AO向下滑动时,端点B会随之自动地沿直线OB向左滑动,如果滑动杆从图中AB处滑动到A′B′处,那么滑动杆的中点C所经过的路径是( )
如图,在直角∠O的内部有一滑动杆AB,当端点A沿直线AO向下滑动时,端点B会随之自动地沿直线OB向左滑动,如果滑动杆从图中AB处滑动到A′B′处,那么滑动杆的中点C所经过的路径是( )| A. | 直线的一部分 | B. | 圆的一部分 | C. | 双曲线的一部分 | D. | 抛物线的一部分 |
19.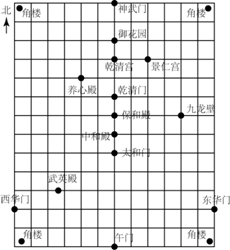 如图是利用平面直角坐标系画出的故宫博物院的主要建筑分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示太和门的点的坐标为(0,-1),表示九龙壁的点的坐标为(4,1),则表示下列宫殿的点的坐标正确的是( )
如图是利用平面直角坐标系画出的故宫博物院的主要建筑分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示太和门的点的坐标为(0,-1),表示九龙壁的点的坐标为(4,1),则表示下列宫殿的点的坐标正确的是( )
 如图是利用平面直角坐标系画出的故宫博物院的主要建筑分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示太和门的点的坐标为(0,-1),表示九龙壁的点的坐标为(4,1),则表示下列宫殿的点的坐标正确的是( )
如图是利用平面直角坐标系画出的故宫博物院的主要建筑分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示太和门的点的坐标为(0,-1),表示九龙壁的点的坐标为(4,1),则表示下列宫殿的点的坐标正确的是( )| A. | 景仁宫(4,2)? | B. | 养心殿(-2,3) | C. | 保和殿(1,0) | D. | 武英殿(-3.5,-4) |
 如图,OA在x轴上,OB在y轴上,OA=8,AB=10,点C在边OA上,AC=2,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数y=$\frac{k}{x}$(k≠0)的图象经过圆心P,则k=-5.
如图,OA在x轴上,OB在y轴上,OA=8,AB=10,点C在边OA上,AC=2,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数y=$\frac{k}{x}$(k≠0)的图象经过圆心P,则k=-5. 如图,在矩形ABCD中.点O在边AB上,∠AOC=∠BOD.求证:AO=OB.
如图,在矩形ABCD中.点O在边AB上,∠AOC=∠BOD.求证:AO=OB.
 如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.求证:∠CBE=∠BAD.
如图,在△ABC中,AB=AC,AD是BC边上的中线,BE⊥AC于点E.求证:∠CBE=∠BAD. 如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则当x=9时,点R应运动到( )
如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则当x=9时,点R应运动到( ) 如图,在直角三角形ABC中,∠ACB=90°,点O在AB上,且CA=CO,若将直角三角形ABC绕着点A顺时针旋转,得到直角三角形AED,B、C的对应点分别为E、D,且点D落在CO的延长线上,连接BE交CO的延长线于点F,若CA=6,AB=18,则BF的长为14.
如图,在直角三角形ABC中,∠ACB=90°,点O在AB上,且CA=CO,若将直角三角形ABC绕着点A顺时针旋转,得到直角三角形AED,B、C的对应点分别为E、D,且点D落在CO的延长线上,连接BE交CO的延长线于点F,若CA=6,AB=18,则BF的长为14.