题目内容
10. 如图,在平行四边形ABCD中,EF∥AB交AD于E,交BD于F,DE:EA=3:4,EF=3,则CD的长为( )
如图,在平行四边形ABCD中,EF∥AB交AD于E,交BD于F,DE:EA=3:4,EF=3,则CD的长为( )| A. | 4 | B. | 7 | C. | 3 | D. | 12 |
分析 由EF∥AB,根据平行线分线段成比例定理,即可求得$\frac{DE}{DA}=\frac{EF}{AB}$,则可求得AB的长,又由四边形ABCD是平行四边形,根据平行四边形对边相等,即可求得CD的长.
解答 解:∵DE:EA=3:4,
∴DE:DA=3:7
∵EF∥AB,
∴$\frac{DE}{DA}=\frac{EF}{AB}$,
∵EF=3,
∴$\frac{3}{7}=\frac{3}{AB}$,
解得:AB=7,
∵四边形ABCD是平行四边形,
∴CD=AB=7.
故选B.
点评 此题考查了平行线分线段成比例定理与平行四边形的性质.此题难度不大,解题的关键是注意数形结合思想的应用.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
18.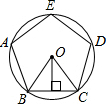 如图,⊙O是正五边形ABCDE的外接圆,这个正五边形的边长为a,半径为R,边心距为r,则下列关系式错误的是( )
如图,⊙O是正五边形ABCDE的外接圆,这个正五边形的边长为a,半径为R,边心距为r,则下列关系式错误的是( )
 如图,⊙O是正五边形ABCDE的外接圆,这个正五边形的边长为a,半径为R,边心距为r,则下列关系式错误的是( )
如图,⊙O是正五边形ABCDE的外接圆,这个正五边形的边长为a,半径为R,边心距为r,则下列关系式错误的是( )| A. | R2-r2=a2 | B. | a=2Rsin36° | C. | a=2rtan36° | D. | r=Rcos36° |
19.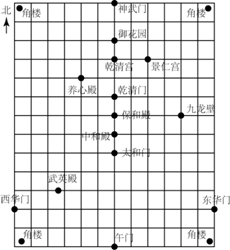 如图是利用平面直角坐标系画出的故宫博物院的主要建筑分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示太和门的点的坐标为(0,-1),表示九龙壁的点的坐标为(4,1),则表示下列宫殿的点的坐标正确的是( )
如图是利用平面直角坐标系画出的故宫博物院的主要建筑分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示太和门的点的坐标为(0,-1),表示九龙壁的点的坐标为(4,1),则表示下列宫殿的点的坐标正确的是( )
 如图是利用平面直角坐标系画出的故宫博物院的主要建筑分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示太和门的点的坐标为(0,-1),表示九龙壁的点的坐标为(4,1),则表示下列宫殿的点的坐标正确的是( )
如图是利用平面直角坐标系画出的故宫博物院的主要建筑分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示太和门的点的坐标为(0,-1),表示九龙壁的点的坐标为(4,1),则表示下列宫殿的点的坐标正确的是( )| A. | 景仁宫(4,2)? | B. | 养心殿(-2,3) | C. | 保和殿(1,0) | D. | 武英殿(-3.5,-4) |
9. 将矩形ABCD绕点B顺时针旋转90°后得到矩形A′BC′D′,若AB=12,AD=5,则△DBD′的面积为( )
将矩形ABCD绕点B顺时针旋转90°后得到矩形A′BC′D′,若AB=12,AD=5,则△DBD′的面积为( )
 将矩形ABCD绕点B顺时针旋转90°后得到矩形A′BC′D′,若AB=12,AD=5,则△DBD′的面积为( )
将矩形ABCD绕点B顺时针旋转90°后得到矩形A′BC′D′,若AB=12,AD=5,则△DBD′的面积为( )| A. | 13 | B. | 26 | C. | 84.5 | D. | 169 |
 如图,一只蚂蚁从O点出发,沿着扇形OAB的边缘匀速爬行一周,当蚂蚁运动的时间为t时,蚂蚁与O点的距离为s,则s关于t的函数图象大致是( )
如图,一只蚂蚁从O点出发,沿着扇形OAB的边缘匀速爬行一周,当蚂蚁运动的时间为t时,蚂蚁与O点的距离为s,则s关于t的函数图象大致是( )



 如图,OA在x轴上,OB在y轴上,OA=8,AB=10,点C在边OA上,AC=2,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数y=$\frac{k}{x}$(k≠0)的图象经过圆心P,则k=-5.
如图,OA在x轴上,OB在y轴上,OA=8,AB=10,点C在边OA上,AC=2,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数y=$\frac{k}{x}$(k≠0)的图象经过圆心P,则k=-5.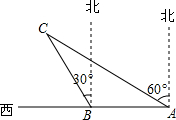 如图,某渔船在海面上朝正西方向以20海里/时匀速航行,在A处观测到灯塔C在北偏西60°方向上,航行1小时到达B处,此时观察到灯塔C在北偏西30°方向上,若该船继续向西航行至离灯塔距离最近的位置,求此时渔船到灯塔的距离(结果精确到1海里,参考数据:$\sqrt{3}$≈1.732)
如图,某渔船在海面上朝正西方向以20海里/时匀速航行,在A处观测到灯塔C在北偏西60°方向上,航行1小时到达B处,此时观察到灯塔C在北偏西30°方向上,若该船继续向西航行至离灯塔距离最近的位置,求此时渔船到灯塔的距离(结果精确到1海里,参考数据:$\sqrt{3}$≈1.732) 如图,在矩形ABCD中.点O在边AB上,∠AOC=∠BOD.求证:AO=OB.
如图,在矩形ABCD中.点O在边AB上,∠AOC=∠BOD.求证:AO=OB.