题目内容
若a：2=b：3=c：7，则
的值是 ．
| 2a-b+3c |
| a+2b |
考点：比例的性质
专题：计算题
分析：设比值为k，然后用k表示出a、b、c，再把a、b、c的值代入代数式进行计算即可得解．
解答：解：设a：2=b：3=c：7=k，
则a=2k，b=3k，c=7k，
所以
=
=
=
．
故答案为：
．
则a=2k，b=3k，c=7k，
所以
| 2a-b+3c |
| a+2b |
| 2×2k-3k+3×7k |
| 2k+2×3k |
| 22k |
| 8k |
| 11 |
| 4 |
故答案为：
| 11 |
| 4 |
点评：本题考查了比例的性质，利用“设k法”表示出a、b、c是解题的关键．
练习册系列答案
开心试卷期末冲刺100分系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
若(a
=
，如5
=
)，x＞1，y＞0，且满足xy=xy，
=x3y，则x+y的值为（ ）
| 1 |
| n |
| n | a |
| 1 |
| 3 |
| 3 | 5 |
| x |
| y |
| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
如图，在一块展示牌上，整齐地贴着许多资料卡片，这些卡片的大小相同，卡片之间露出了三个正方形的空白（图中阴影部分），已知卡片的短边长度是12cm．现要将这三个正方形的空白用三张图片填补，则一张图片的边长应为已知|a|=5，
=3，且ab＜0，则a-b=（ ）
| b2 |
| A、8 | B、-2 |
| C、8或-8 | D、2或-2 |
如图：AB、CD相交于O，且∠A=∠C，若OA=2，OD=3，OB=1，则OC=
如图，AD⊥AB于A，BE⊥AB于B，点C在AB上，且CD⊥CE，CD=CE．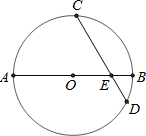
如图，AB是⊙O的直径，弦CD与AB相交于点E，AE=13，BE=3，cos∠AEC=