题目内容
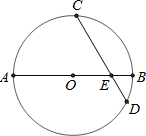如图，AB是⊙O的直径，弦CD与AB相交于点E，AE=13，BE=3，cos∠AEC=| 3 |
| 5 |
考点：垂径定理,解直角三角形
专题：
分析：作OM⊥CD于点M，连接OC，在直角三角形OEM中，根据三角函数求得OM的长，然后在直角△OCM中，利用勾股定理即可求得CM的长，进而求得CD的长．
解答：
解：作OM⊥CD于点M，连接OC．
∵AE=13，BE=3，
∴OC=OA=OB=
（AE+BE）=8，
∴OE=OB-BE=8-3=5．
在Rt△OME中，cos∠AEC=
=
，
解得，EM=3，
∴OM=4，
在Rt△OCM中，CM=
=4
，
∴CD=2CM=8
．
解：作OM⊥CD于点M，连接OC．∵AE=13，BE=3，
∴OC=OA=OB=
| 1 |
| 2 |
∴OE=OB-BE=8-3=5．
在Rt△OME中，cos∠AEC=
| 3 |
| 5 |
| EM |
| OE |
解得，EM=3，
∴OM=4，
在Rt△OCM中，CM=
| OC2-OM2 |
| 3 |
∴CD=2CM=8
| 3 |
点评：本题考查了垂径定理，以及勾股定理，正确求得OM的长是关键．
练习册系列答案
黄冈创优卷系列答案
相关题目
如图，点A、B、C是方格纸上的格点，若最小方格的边长为1，则△ABC的面积为（ ）| A、6 | B、8 | C、12 | D、16 |
下列方程中，无实数根的方程是（ ）
| A、x2-3x+2=0 | ||
| B、（x-3）2+2=x2 | ||
C、
| ||
D、
|
如图所示，矩形ABCD中，AB=2，BC=3，P为BC边上与BC两点不重合的任意一点．设PA=x，D到PA的距离为y，则y与x的函数关系式为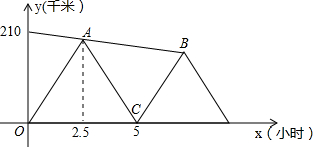
步行速度均近似为匀速，队员上、下车的时间忽略不计）．