题目内容
 如图:AB、CD相交于O,且∠A=∠C,若OA=2,OD=3,OB=1,则OC=
如图:AB、CD相交于O,且∠A=∠C,若OA=2,OD=3,OB=1,则OC=考点:相似三角形的判定与性质
专题:计算题
分析:由已知的一对角相等,加上一对对顶角相等,利用两对对应角相等的两三角形相似可得出三角形AOD与三角形COB相似,根据相似三角形的对应边成比例列出关系式,将已知的OA,OB,以及OD的长代入,即可求出OC的长.
解答:解:∵∠A=∠C,∠AOD=∠COB(对顶角相等),
∴△AOD∽△COB,
∴
=
,又OA=2,OD=3,OB=1,
则OC=
=
.
故答案为:
∴△AOD∽△COB,
∴
| OA |
| OC |
| OD |
| OB |
则OC=
| OA•OB |
| OD |
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |
点评:此题考查了相似三角形的判定与性质,相似三角形的判定方法有:两对对应角相等的两三角形相似;两边对应成比例且夹角相等的两三角形相似;三边对应成比例的两三角形相似,以及相似三角形的定义,熟练掌握相似三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
直线L1过点B(0,1)与点A(-1,0),求直线L1的函数解析式是( )
| A、y=-3x-2 |
| B、y=-x |
| C、y=x+1 |
| D、y=-2x+1 |
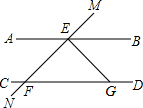 如图,两平行直线AB和CD被直线MN所截,交点分别为E、F,点G为射线FD上的一点,且EF=EG,若∠EFG=45°,则∠BEG为( )
如图,两平行直线AB和CD被直线MN所截,交点分别为E、F,点G为射线FD上的一点,且EF=EG,若∠EFG=45°,则∠BEG为( )| A、30° | B、45° |
| C、60° | D、90° |
 如图,点A、B、C是方格纸上的格点,若最小方格的边长为1,则△ABC的面积为( )
如图,点A、B、C是方格纸上的格点,若最小方格的边长为1,则△ABC的面积为( )| A、6 | B、8 | C、12 | D、16 |
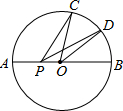 如图,已知⊙O的半径为R,C、D是直径AB的同侧圆周上的两点,
如图,已知⊙O的半径为R,C、D是直径AB的同侧圆周上的两点,
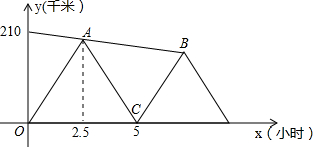 步行速度均近似为匀速,队员上、下车的时间忽略不计).
步行速度均近似为匀速,队员上、下车的时间忽略不计).