题目内容
 如图,AD⊥AB于A,BE⊥AB于B,点C在AB上,且CD⊥CE,CD=CE.
如图,AD⊥AB于A,BE⊥AB于B,点C在AB上,且CD⊥CE,CD=CE.求证:AB=AD+BE.
考点:全等三角形的判定与性质
专题:证明题
分析:根据直角三角形的性质推出∠D=∠BCE,然后利用角角边证明△ACD和△BEC全等,再根据全等三角形对应边相等得到AD=BC,AC=BE,最后根据AB=AC+BC,等量代换即可得证.
解答:证明:∵AD⊥AB,BE⊥AB,
∴∠A=∠B=90°,
∴∠D+∠ACD=90°,
∵CD⊥CE,
∴∠ACD+∠BCE=180°-90°=90°,
∴∠D=∠BCE,
在△ACD和△BEC中,
,
∴△ACD≌△BEC(AAS),
∴AD=BC,AC=BE,
又∵AB=AC+BC,
∴AB=AD+BE.
∴∠A=∠B=90°,
∴∠D+∠ACD=90°,
∵CD⊥CE,
∴∠ACD+∠BCE=180°-90°=90°,
∴∠D=∠BCE,
在△ACD和△BEC中,
|
∴△ACD≌△BEC(AAS),
∴AD=BC,AC=BE,
又∵AB=AC+BC,
∴AB=AD+BE.
点评:本题考查了全等三角形的判定与性质,根据直角三角形的性质以及平角等于180°证明得到∠D=∠BCE是证明三角形全等的关键,也是本题的难点.

练习册系列答案
相关题目
 其解集如数轴上所示的不等式组是( )
其解集如数轴上所示的不等式组是( )A、
| |||||
B、
| |||||
C、
| |||||
D、
|
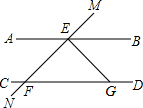 如图,两平行直线AB和CD被直线MN所截,交点分别为E、F,点G为射线FD上的一点,且EF=EG,若∠EFG=45°,则∠BEG为( )
如图,两平行直线AB和CD被直线MN所截,交点分别为E、F,点G为射线FD上的一点,且EF=EG,若∠EFG=45°,则∠BEG为( )| A、30° | B、45° |
| C、60° | D、90° |
 如图,点A、B、C是方格纸上的格点,若最小方格的边长为1,则△ABC的面积为( )
如图,点A、B、C是方格纸上的格点,若最小方格的边长为1,则△ABC的面积为( )| A、6 | B、8 | C、12 | D、16 |