题目内容
17.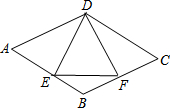 如图,已知菱形ABCD中,E是AB的中点,且DE⊥AB于E,设AB=a.求:
如图,已知菱形ABCD中,E是AB的中点,且DE⊥AB于E,设AB=a.求:(1)∠ABC的度数;
(2)对角线AC的长.
分析 (1)首先连接BD,由E是AB的中点,且DE⊥AB,根据线段垂直平分线的性质,可得AD=BD,又由菱形ABCD,可得AB=AD,即可判定△ABD是等边三角形,继而求得答案;
(2)首先由(1)可求得BD的长,再由菱形的性质,求得OB的长,利用勾股定理即可求得OA的长,继而求得答案.
解答 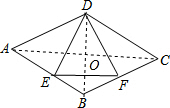 解:(1)连接BD,
解:(1)连接BD,
∵四边形ABCD是菱形,
∴AD=AB,
∵E是AB的中点,且DE⊥AB,
∴AD=BD,
∴AD=AB=BD,
∴△ABD是等边三角形,
∴∠ABD=60°,
∴∠ABC=2∠ABD=120°;
(2)连接AC,交BD于点O,
∵△ABD是等边三角形,
∴BD=AB=a,
∵四边形ABCD是菱形,
∴AC⊥BD,OB=$\frac{1}{2}$BD=$\frac{1}{2}$a,
∴OA=$\sqrt{A{B}^{2}-O{B}^{2}}$=$\frac{\sqrt{3}}{2}$a,
∴AC=2OA=$\sqrt{3}$a.
点评 此题考查了菱形的性质、等边三角形的判定与性质以及勾股定理.注意证得△ABD是等边三角形是关键.

练习册系列答案
相关题目
2.现有大、小两种船,1艘大船与4艘小船一次最多可以载客46名,2艘大船与3艘小船一次最多可以载客57名,某旅游点的船有3艘大船与6艘小船,一次最多可以载客的人数为( )
| A. | 129 | B. | 120 | C. | 108 | D. | 96 |
7.下列计算正确的是( )
| A. | m3-m2=m | B. | -(-3)=3 | C. | (m+n)2=m2+n2 | D. | (3x)2=6x2 |
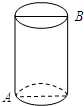 如图所示,有一个圆柱体,高为12cm,底面半径为3cm,在圆柱下底面A处有一只蜘蛛.它想到上底面B处捉住一只苍蝇,则蜘蛛所走的最短路线长应为6$\sqrt{5}$cm(π取3.0).
如图所示,有一个圆柱体,高为12cm,底面半径为3cm,在圆柱下底面A处有一只蜘蛛.它想到上底面B处捉住一只苍蝇,则蜘蛛所走的最短路线长应为6$\sqrt{5}$cm(π取3.0).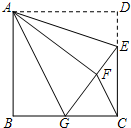 如图,正方形ABCD中,CD=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.
如图,正方形ABCD中,CD=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.